解:(1)由题意可知:f'(x)=lnx-1,令f'(x)=0,得x=e,(1分)
则当x∈(0,e)时,f′(x)<0,f(x)单调递减;(2分)
当x∈(e,+∞)时,f′(x)>0,f(x)单调递增(4分)
(2)由(1)可得f(x)在x=e处取得极小值,且f(x)=0没有实根,(6分)
则minf(x)=f(e)>0,即a-e>0,解得:a>e(8分)
(3)方法1:由(2)得,令a=3>e,f(x)=xlnx-2x+3>0成立,
则?x>0,xlnx>2x-3恒成立(10分)
故ln1+2ln2+3ln3++nlnn=2ln2+3ln3++nlnn>(2•2-3)+(2•3-3)+(2•4-3)++(2•n-3)=
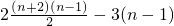
=(n-1)
2,即得证.(14分)
方法2:数学归纳法
(1)当n=2(2)时,ln1+2ln2>1
2(3)成立;
(4)当n=k(5)时,ln1+2ln2+3ln3++klnk>(k-1)
2(6)成立,
当n=k+1时,ln1+2ln2+3ln3++klnk+(k+1)ln(k+1)>(k-1)
2+(k+1)ln(k+1)
同理令a=3>e,xlnx>2x-3,即(k+1)ln(k+1)>2(k+1)-3,(10分)
则(k-1)
2+(k+1)ln(k+1)>(k-1)
2+2(k+1)-3=k
2,(12分)
故ln1+2ln2+3ln3++klnk+(k+1)ln(k+1)>k
2,
即ln1+2ln2+3ln3++klnk>(k-1)
2对n=k+1也成立,
综合(1)(2)得:?n≥2,ln1+2ln2+3ln3++nlnn>(n-1)
2恒成立.(14分)
分析:(1)利用导数求出函数的极值,然后求f(x)的单调区间;
(2)若方程f(x)=0没有实根,由(1)可得f(x)在x=e处取得极小值,且f(x)=0没有实根,即可求a的取值范围;
(3)方法一:利用?x>0,xlnx>2x-3恒成立,即可证明ln1+2ln2+3ln3+…+nlnn>(n-1)
2.
方法二:利用数学归纳法验证n=2成立,然后通过假设,证明n=k+1不等式也成立即可.
点评:本题是中档题,考查函数的导数的应用,不等式的综合应用,数学归纳法的应用,考查计算能力,转化思想的应用.

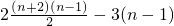 =(n-1)2,即得证.(14分)
=(n-1)2,即得证.(14分)

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<