
����Ŀ��2000����ǰ����ϣ������ѧ�Ұ��������˹((Apollonius)���֣�ƽ���Բ�Ľؿ�������Բ����.��֪Բ�ĸ�Ϊ![]() ��
�� ![]() Ϊ����ֱ��������Ϊ
Ϊ����ֱ��������Ϊ![]() ����ô��������
����ô��������![]() ��ƽ�棻��
��ƽ�棻��![]() �н�
�н�![]() ʱ���ؿ�����Ϊ��Բ����
ʱ���ؿ�����Ϊ��Բ����![]() �н�
�н�![]() ʱ���ؿ�����Ϊ�����ߣ���
ʱ���ؿ�����Ϊ�����ߣ���![]() �н�
�н�![]() ʱ���ؿ�����Ϊ˫����.��ͼ�������ڵ�ֱ��
ʱ���ؿ�����Ϊ˫����.��ͼ�������ڵ�ֱ��![]() ����
����![]() ��ƽ���Բ�õ�������Ϊ��Բ��������
��ƽ���Բ�õ�������Ϊ��Բ��������![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ����֪
����֪![]() Ϊ����.��ô��
Ϊ����.��ô��![]() ���߶�
���߶�![]() ���˶�ʱ���ؿ����ߵĶ��ᶥ��Ĺ켣Ϊ�� ��
���˶�ʱ���ؿ����ߵĶ��ᶥ��Ĺ켣Ϊ�� ��
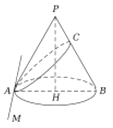
A. Բ�IJ��� B. ��Բ�IJ��� C. ˫���ߵIJ��� D. �����ߵIJ���

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������װ��5�ű������Ϊ1��2��3��4��5�Ŀ�Ƭ����5�ſ�Ƭ����������ȫ��ͬ���ֽ����зŻص�������ȡ���Σ�ÿ�������ȡ��һ�ſ�Ƭ��
��1��������п��ܽ���������г����п��ܽ����
��2����������ȡ����Ƭ�ĺ���֮�Ͳ�С��7��С��5���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x���ĵ�����f�䣨x���Ƕ��κ�������ͼ��f�䣨x���Ĵ���ͼ����f��x���ļ���ֵ�뼫Сֵ�ĺ͵��� ![]() ����f��0����ֵΪ�� ��
����f��0����ֵΪ�� ��
A.0
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��4��23������������գ�Ϊ���ѧ���Զ�������ӣ��ø�����˳������麣�У��Ӷ��ջ�����֪ʶ��ij���е�Уѧ���Ὺչ������Ϊ�����Ķ���Ϊϰ�ߣ���˼��������������ʵ�����Уѧ����ʵ������ͬѧ�漴�����ѧУ��40����һѧ����ͨ������������ϲ����ֽ���黹��ϲ���������飬���˽���У��һѧ���Ķ���ϰ�ߣ��õ������������
ϲ����ֽ���� | ��ϲ����ֽ���� | �ϼ� | |
�� | 16 | 4 | 20 |
Ů | 8 | 12 | 20 |
�ϼ� | 24 | 16 | 40 |
����������������ܷ���99%�İ�����Ϊ�Ƿ�ϲ����ֽ���鼮���Ա��й�ϵ��
�������ӱ�����16����ϲ����ֽ���鼮��ѧ���������ȡ2��ѧ������鵽�����������ķֲ��м�����ѧ����E���Σ���
�ο���ʽ��K2=![]() ������n=a+b+c+d��
������n=a+b+c+d��
���е��ٽ�ֵ�����ο���
P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĸ���������������������ǣ�������
��Ϊ���˽�800��ѧ���ijɼ���������г�ȡһ������Ϊ40��������������ϵͳ��������ֶεļ��kΪ40��
�����Իع�ֱ��![]() ��������������
��������������![]() ��
��
�����������������̬�ֲ�N��2����2��������0�������ڣ�������1����ȡֵ�ĸ���Ϊ0.1�����ڣ�2��3���ڵĸ���Ϊ0.4��
�����¼�![]() ��
��![]() �����ϵ
�����ϵ![]() �����¼�
�����¼�![]() ��
��![]() ���⣮
���⣮
A. 0 B. 1 C. 2 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲM��Բ��ΪM����1��2����ֱ��y=x+4��ԲM�صõ��ҳ�Ϊ ![]() ����P��ֱ��l��y=x��1�ϣ�
����P��ֱ��l��y=x��1�ϣ�
��1����ԲM�ı����̣�
��2�����Q��ԲM�ϣ������� ![]() =4
=4 ![]() �����P�����ꣻ
�����P�����ꣻ
��3����뾶Ϊ5��ԲN��ԲM���룬����P�ֱ���ԲM��ԲN�����ߣ��е�ֱ�ΪA��B����������ĵ�P������PA=PB��������Բ��N�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ![]() ������֪��Բ
������֪��Բ![]() ����Ϊ
����Ϊ![]() ��������Ϊ
��������Ϊ![]() ������
������![]() �Ҵ�ֱ�ڳ�����ҳ�Ϊ
�Ҵ�ֱ�ڳ�����ҳ�Ϊ![]() ��
��
��1������Բ![]() �ı����̣�
�ı����̣�
��2�����![]() �ֱ�����Բ�����Ҷ�����������
�ֱ�����Բ�����Ҷ�����������![]() ��ֱ������Բ�ཻ�ڲ�ͬ����
��ֱ������Բ�ཻ�ڲ�ͬ����![]() ��
��
����֤��![]() ��
��
����![]() ���������ֵ��
���������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ�鱭������������������̭������ij��������һ��������ڳ���ʱ����սƽ��ֱ�ӽ�������ʤ���ڣ��ڵ����ʤ�����У�˫�������������������֣����и���������ӻ�ʤ����˫�������ַ�����δ��ʤ��������Ҫ����һ��һ�ĵ����ʤ����˫�����ɴ�һ����Ա������ֱ���ֳ�ʤ������ǰ���ַ����У���ijһʱ��ʤ���ѷ֣���δ�����Ķ�Ա���������������һ�����ȷ��������£�һ��ǰ���־����У�����ǰ����δ�����У���һ�ࡢ����ĵ���λͬѧ���������.����һ��ͬѧƽʱ��������ϸߣ�ÿλ��Ա������������ʶ��ܴﵽ0.8���������Ա�ĵ������д�ֻ��0.5������ʱͨ����ǩ����һ����ÿһ�ֶ��ȷ���.
��1�������¼�![]() Ϊ��һ�����λͬѧû�ܳ����������¼�
Ϊ��һ�����λͬѧû�ܳ����������¼�![]() �����ĸ��ʣ�
�����ĸ��ʣ�
��2����������ǰ���ֵ���������ƽ�������һ��һ�����ʤ��һ��һ���ʤ��û����֮ǰ�����ս�г������Ķ�Ա������������һ��һ�����ʤ��ijһ���У�ij�Զ�Ա�����������һ��Աδ�����룬�������������������Ա��������߾���ʧ�����������һ�ֱ���. ��ֱ��˫������ÿ����Ա���Ѿ���������������������˫��ͨ����ǩ����ʤ������������������֪˫���ڵ����ս�����������![]() ��¼˫������һ��һ�����ʤ����������
��¼˫������һ��һ�����ʤ����������![]() �ķֲ�������ѧ����.
�ķֲ�������ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ�鱭������������������̭������ij��������һ��������ڳ���ʱ����սƽ��ֱ�ӽ�������ʤ���ڣ��ڵ����ʤ�����У�˫�������������������֣����и���������ӻ�ʤ����˫�������ַ�����δ��ʤ��������Ҫ����һ��һ�ĵ����ʤ����˫�����ɴ�һ����Ա������ֱ���ֳ�ʤ������ǰ���ַ����У���ijһʱ��ʤ���ѷ֣���δ�����Ķ�Ա���������������һ�����ȷ��������£�һ��ǰ���־����У�����ǰ����δ�����У���һ�ࡢ����ĵ���λͬѧ���������.����һ��ͬѧƽʱ��������ϸߣ�ÿλ��Ա������������ʶ��ܴﵽ0.8���������Ա�ĵ������д�ֻ��0.5������ʱͨ����ǩ����һ����ÿһ�ֶ��ȷ���.
��1�������¼�![]() Ϊ��һ�����λͬѧû�ܳ����������¼�
Ϊ��һ�����λͬѧû�ܳ����������¼�![]() �����ĸ��ʣ�
�����ĸ��ʣ�
��2����������ǰ���ֵ���������ƽ�������һ��һ�����ʤ��һ��һ���ʤ��û����֮ǰ�����ս�г������Ķ�Ա������������һ��һ�����ʤ��ijһ���У�ij�Զ�Ա�����������һ��Աδ�����룬�������������������Ա��������߾���ʧ�����������һ�ֱ���. ��ֱ��˫������ÿ����Ա���Ѿ���������������������˫��ͨ����ǩ����ʤ������������������֪˫���ڵ����ս�����������![]() ��¼˫������һ��һ�����ʤ����������
��¼˫������һ��һ�����ʤ����������![]() �ķֲ�������ѧ����.
�ķֲ�������ѧ����.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com