
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | 3 |
分析 求出角的范围,化简所求表达式,利用三角函数的平方以及二倍角公式化简求解即可.
解答 解:sin2θ=$\frac{3}{5}$,且0<2θ<$\frac{π}{2}$,可得$0<θ<\frac{π}{4}$,
$\frac{2co{s}^{2}\frac{θ}{2}-sinθ-1}{\sqrt{2}sin(θ+\frac{π}{4})}$=$\frac{cosθ-sinθ}{sinθ+cosθ}$=$\sqrt{({\frac{cosθ-sinθ}{sinθ+cosθ})}^{2}}$=$\sqrt{\frac{1-\frac{3}{5}}{1+\frac{3}{5}}}$=$\frac{1}{2}$.
故选:C.
点评 本题考查三角函数化简求值,二倍角公式的应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | -6 | C. | 6 | D. | -2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22015-1 | B. | 22016-2 | C. | 22014-1 | D. | 1-22015 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
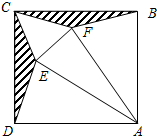 如图,将正方形剪去两个底角为15°的等腰三角形CDE和CBF,然后沿图中所画的线折成一个正三棱锥,这个正三棱锥侧面与底面所成的二面角的余弦值为$\frac{2\sqrt{3}}{3}-1$.
如图,将正方形剪去两个底角为15°的等腰三角形CDE和CBF,然后沿图中所画的线折成一个正三棱锥,这个正三棱锥侧面与底面所成的二面角的余弦值为$\frac{2\sqrt{3}}{3}-1$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com