
����Ŀ��ij�������й�����A,B,C,D�����²�Ʒ��Ϊ�˽��²�Ʒ������������ó������������15λ�˿ͣ���Ϊ![]() �������������²�Ʒ���������¼���£���λ��������
�������������²�Ʒ���������¼���£���λ��������
�� �� �� Ʒ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A | 1 | 1 | 1 | 1 | 1 | ||||||||||
B | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
C | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||
D | 1 | 1 | 1 | 1 | 1 | 1 |
�������ó���ÿ��Ŀ�����ԼΪ300�˴Σ�һ���°�30����㣬�Թ��Ʋ�ƷA��������������λ��������
����Ϊ�ƹ��²�Ʒ�����������������ϣ������֣��²�Ʒ�Ĺ˿�����2Ԫ���Ӻ��.���мס��ҡ��������ڸó��й�������ǻ�õĵ��Ӻ�����ܽ��ΪX��
���������X�ķֲ��к���ѧ������
������ij�˿���ѡ�в�ƷB��Ϊ��߳�������ҵ����Ӧ�������Ƽ������²�Ʒ�����������Ҫ֤����
���𰸡���1��3000��2����������3����ƷD .
���������������: ��1���ò�ƷA��Ƶ��������������,��������,�ٳ����������ɹ��Ʋ�ƷA����������; ��2���˿������֣������֣������²�Ʒ�ĸ���Ϊ![]() , X��ȡ0��2��4��6 ,�ֱ���������,�г��ֲ��в��������ֵ; ��3����ƷD .
, X��ȡ0��2��4��6 ,�ֱ���������,�г��ֲ��в��������ֵ; ��3����ƷD .
�������:������![]() ��������
��������
�𣺲�ƷA����������ԼΪ3000��.
���˿������֣������֣������²�Ʒ�ĸ���Ϊ![]() .
.
X��ȡ0��2��4��6 ��
![]() ��
�� ![]() ��
��
![]() ��
�� ![]() ��
��
����X�ķֲ���Ϊ��
X | 0 | 2 | 4 | 6 |
P |
|
|
|
|
����![]() .
.
����ƷD .


 ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ͬ����ϰ����ʦ����ѧ������ϵ�д�
ͬ����ϰ����ʦ����ѧ������ϵ�д� ����ϰ�⽭��ϵ�д�
����ϰ�⽭��ϵ�д� ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]()
![]() ��������Ϊ
��������Ϊ![]() ����ԭ��ΪԲ�ģ���ԲC�Ķ̰��᳤Ϊ�뾶��Բ��ֱ��
����ԭ��ΪԲ�ģ���ԲC�Ķ̰��᳤Ϊ�뾶��Բ��ֱ��![]() ����.
����.![]() ��
��![]() ����Բ�����Ҷ��㣬ֱ��
����Բ�����Ҷ��㣬ֱ��![]() ��
��![]() ������
������![]() �ᴹֱ.
�ᴹֱ.
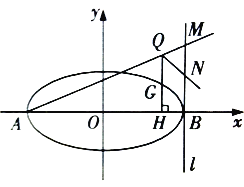
��1������Բ![]() �ı����̣�
�ı����̣�
��2����![]() ����Բ
����Բ![]() ������
������![]() ��
��![]() ������һ�㣬��
������һ�㣬��![]() ���ڵ�
���ڵ�![]() ���ӳ�
���ӳ�![]() ����
����![]() ʹ��
ʹ��![]() ������
������![]() ���ӳ���ֱ��
���ӳ���ֱ��![]() �ڵ�
�ڵ�![]() ��
��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬�ж�ֱ��
���е㣬�ж�ֱ��![]() ����
����![]() Ϊֱ����Բ
Ϊֱ����Բ![]() ��λ�ù�ϵ����֤����Ľ���.
��λ�ù�ϵ����֤����Ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������y2��2px��p>0���Ľ�����б��Ϊ2![]() ��ֱ�߽���������A��x1��y1����B��x2��y2����x1<x2����������|AB|��9��
��ֱ�߽���������A��x1��y1����B��x2��y2����x1<x2����������|AB|��9��
��1����������ߵķ�����
��2��OΪ����ԭ����CΪ��������һ������![]() ����˵�ֵ
����˵�ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC��Բ����ֱ��l��y=2x�ϣ��Ҿ�����A����3����1����B��4��6����
��������ԲC�ķ��̣�
��������P��ֱ��l�Ϻ�����Ϊ��4�ĵ㣬����P��ԲC�����ߣ������߷��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x���Ƕ����ڣ����ޣ�+�ޣ��ϵ�ż���������ڣ����ޣ�0]��������������a=f��log47����b=f��log ![]() 3����c=f��21.6������a��b��c�Ĵ�С��ϵ�ǣ� ��
3����c=f��21.6������a��b��c�Ĵ�С��ϵ�ǣ� ��
A.c��a��b
B.c��b��a
C.b��c��a
D.a��b��c
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
�� ![]() ������
������![]() �ϵĶ���
�ϵĶ���![]() ���㣺
���㣺
![]() .
.
��1��������![]() �ķ��̣�
�ķ��̣�
��2����![]() Ϊ����ԭ�㣬��һ���ĵ�
Ϊ����ԭ�㣬��һ���ĵ�![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ�
�ϣ� ![]() �����߶�
�����߶�![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��,
��, ![]() �ɵȲ�������
�ɵȲ�������![]() ��( )
��( )
A. ��ֲ���Ҫ���� B. ��Ҫ��������� C. ��Ҫ���� D. �Ȳ����Ҳ����Ҫ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ,������Ϊ
,������Ϊ![]() ,��
,��![]() ����Բ������һ��,
����Բ������һ��, ![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() .
.
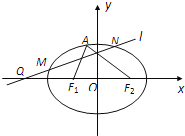
(��)����Բ![]() �ķ��̣�
�ķ��̣�
(��)����![]() (-4,0)����һ��ֱ��
(-4,0)����һ��ֱ��![]() ����Բ
����Բ![]() ��
��![]() ����,��
����,��![]() ,�����߶�
,�����߶�![]() ��ȡһ��
��ȡһ��![]() ,ʹ��
,ʹ��![]() ,��ֱ��
,��ֱ��![]() ת��ʱ,��
ת��ʱ,��![]() ��ijһ��ֱ�����˶�,��ö�ֱ�ߵķ��̣�
��ijһ��ֱ�����˶�,��ö�ֱ�ߵķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ʱ���ж�
ʱ���ж�![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����![]() ��
��![]() ��Ϊ��������������ʵ��
��Ϊ��������������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com