Question

【题目】若一条直线a与平面α内的一条直线b所成的角为30°，则下列说法正确的是(　　)

A. 直线a与平面α所成的角为30° B. 直线a与平面α所成的角大于30°

C. 直线a与平面α所成的角小于30° D. 直线a与平面α所成的角不超过30°

Answer 1

【答案】D

【解析】

根据题意，作出图形如图所示．由直线与平面所成角的定义，得到a与b所成角的最小值等于，最大值等于90°．由此得到本题的答案．

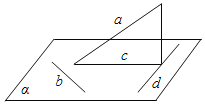
设直线a在平面α的射影为直线c，在平面α内作直线d⊥c，由三垂线定理可得直线d⊥a．

设直线a与平面α所成的角为，

∴直线a与直线c所成的角为，等于平面α内的直线与直线a所成角的最小值．

直线b在平面α内，当b与直线d平行或重合时，可得a⊥b，直线a与b所成的角为90°，达到最大值；

当b与直线c平行或重合时，可得a、b所成的角为，达到最小值．

因此，直线a与b所成的角为φ的取值范围为≤φ≤90°．

因为直线a与平面α内的一条直线b所成的角为30°，

直线a与平面α所成的角不超过30°,

故答案为：D