
【题目】已知公比不为1的等比数列{an}的前5项积为243,且2a3为3a2和a4的等差中项.
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足bn=bn﹣1log3an+2(n≥2且n∈N*),且b1=1,求数列 ![]() 的前n项和Sn .
的前n项和Sn .
【答案】
(1)解:由前5项积为243,即为a1a2a3a4a5=243,
即有a1a5=a2a4=a32,即a35=243,
得:a3=3,设等比数列的公比为q,
由2a3为3a2和a4的等差中项得:4a3=3a2+a4,
即 ![]() ,
,
由公比不为1,解得:q=3,
所以an=a3qn﹣3,
即 ![]()
(2)解:由bn=bn﹣1log3an+2=bn﹣1n,
得 ![]() ,
,
数列 ![]() ,
,
所以它的前n项和 ![]()
【解析】(1)运用等比数列的性质可得a3=3,设等比数列的公比为q,运用等差数列中项的性质,结合等比数列通项公式,解得q=3,即可得到所求数列{an}的通项公式;(2)求得bn=bn﹣1log3an+2=bn﹣1n,运用数列恒等式bn=b1 ![]() …
… ![]() =n!,求出
=n!,求出 ![]() ,运用裂项相消求和即可得到所求和.
,运用裂项相消求和即可得到所求和.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴,建立极坐标系.曲线C1的极坐标方程为ρ=4cosθ,直线l: 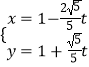 (
( ![]() 为参数).
为参数).
(1)求曲线C1的直角坐标方程及直线l的普通方程;
(2)若曲线C2的参数方程为 ![]() (α为参数),曲线P(x0 , y0)上点P的极坐标为
(α为参数),曲线P(x0 , y0)上点P的极坐标为 ![]() ,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F(1,0),点A是直线l1:x=﹣1上的动点,过A作直线l2 , l1⊥l2 , 线段AF的垂直平分线与l2交于点P.
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)若点M,N是直线l1上两个不同的点,且△PMN的内切圆方程为x2+y2=1,直线PF的斜率为k,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义域为(0,+∞)的单调函数,若对任意的x∈(0,+∞),都有 ![]() ,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,则实数a的取值范围是( )
,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,则实数a的取值范围是( )
A.0<a≤5
B.a<5
C.0<a<5
D.a≥5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D. 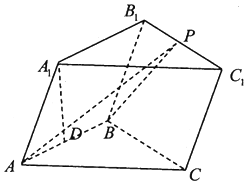
(1)证明:平面AA1B1B⊥平面BB1C1C;
(2)设P为B1C1上一点,且 ![]() ,求二面角A1﹣AB﹣P的正弦值.
,求二面角A1﹣AB﹣P的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.已知点
轴的正半轴为极轴建立极坐标系.已知点![]() 的直角坐标为
的直角坐标为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 过点
过点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() ,求直线
,求直线![]() 的直角坐标方程.
的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂新研发了一种产品,该产品每件成本为5元,将该产品按事先拟定的价格进行销售,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求销量![]() (件)关于单价
(件)关于单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;
;
(2)若单价定为10元,估计销量为多少件;
(3)根据销量![]() 关于单价
关于单价![]() 的线性回归方程,要使利润
的线性回归方程,要使利润![]() 最大,应将价格定为多少?
最大,应将价格定为多少?
参考公式: ,
,![]() .参考数据:
.参考数据:![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com