练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，在直三棱柱ABCA1B1C1中，已知∠ACB＝90°，M为A1B与AB1的交点，N为棱B1C1的中点．

    (1)求证：MN∥平面AA1C1C；

    (2)若AC＝AA1，求证：MN⊥平面A1BC.

     

    （1）见解析（2）见解析

    【解析】证明：(1)连结AC1，因为M为A1B与AB1的交点，所以M是AB1的中点．又N为棱B1C1的中点，所以MN∥AC1.又AC1平面AA1C1C，MN平面AA1C1C，所以MN∥平面AA1C1C.

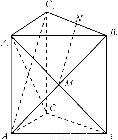
    (2)由AC＝AA1，则四边形AA1C1C是正方形，所以AC1⊥A1C.因为ABCA1B1C1是直三棱柱，所以CC1⊥平面ABC.因为BC平面ABC，所以CC1⊥BC.因为∠ACB＝90°，所以AC⊥BC.因为CC1∩AC＝C，所以BC⊥平面AA1C1C，所以BC⊥AC1.又AC1平面AA1C1C，MN∥AC1，所以MN⊥A1C，MN⊥BC.又BC∩A1C＝C，所以MN⊥平面A1BC.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第六章第1课时练习卷（解析版） 题型：解答题

    已知关于x的不等式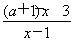：<1.

    (1)当a＝1时，解该不等式；

    (2)当a>0时，解该不等式．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第八章第5课时练习卷（解析版） 题型：填空题

    如图所示，正方体ABCDA1B1C1D1的棱长为6，则以正方体ABCDA1B1C1D1的中心为顶点，以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为________．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第八章第4课时练习卷（解析版） 题型：解答题

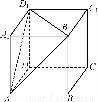
    如图，直三棱柱ABC－A1B1C1中，D、E分别是棱BC、AB的中点，点F在棱CC1上，已知AB＝AC，AA1＝3，BC＝CF＝2.

    (1)求证：C1E∥平面ADF；

    (2)设点M在棱BB1上，当BM为何值时，平面CAM⊥平面ADF?

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第八章第4课时练习卷（解析版） 题型：填空题

    设a、b为不重合的两条直线，α、β为不重合的两个平面，给出下列命题：

    ①若a∥α且b∥α，则a∥b；②若a⊥α且b⊥α，则a∥b；③若a∥α且a∥β，则α∥β；④若a⊥α且a⊥β，则α∥β.其中为真命题的是________．(填序号)

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷（解析版） 题型：解答题

    由平面α外一点P引平面的三条相等的斜线段，斜足分别为A、B、C，O为△ABC的外心，求证：OP⊥α.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷（解析版） 题型：填空题

    P为△ABC所在平面外一点，O为P在平面ABC内的射影．

    (1)若P到△ABC三边距离相等，且O在△ABC的内部，则O是△ABC的________心；

    (2)若PA⊥BC，PB⊥AC，则O是△ABC的________心；

    (3)若PA，PB，PC与底面所成的角相等，则O是△ABC的________心．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第八章第2课时练习卷（解析版） 题型：填空题

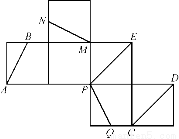
    如图是一正方体的表面展开图，B、N、Q都是所在棱的中点，则在原正方体中，①AB与CD相交；②MN∥PQ；③AB∥PE；④MN与CD异面；⑤MN∥平面PQC.

    其中真命题的是________(填序号)．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第5课时练习卷（解析版） 题型：解答题

    我国是一个人口大国，随着时间推移，老龄化现象越来越严重，为缓解社会和家庭压力，决定采用养老储备金制度．公民在就业的第一年交纳养老储备金，数目为a1，以后每年交纳的数目均比上一年增加d(d>0)，因此，历年所交纳的储备金数目a1，a2，…，an是一个公差为d的等差数列．与此同时，国家给予优惠的计息政策，不仅采用固定利率，而且计算复利．这就是说，如果固定利率为r(r>0)，那么，在第n年末，第一年所交纳的储备金就变为a1(1＋r)n－1，第二年所交纳的储备金就变为a2(1＋r)n－2，…，以Tn表示到第n年所累计的储备金总额．

    (1)写出Tn与Tn－1(n≥2)的递推关系式；

    (2)求证：Tn＝An＋Bn，其中{An}是一个等比数列，{Bn}是一个等差数列．

     

    查看答案和解析>>

    同步练习册答案