
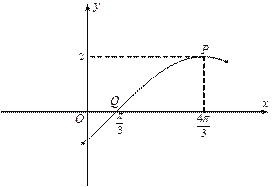
【题目】如图为函数![]() 图像的一部分,其中点
图像的一部分,其中点![]() 是图像的一个最高点,点
是图像的一个最高点,点![]() 是与点
是与点![]() 相邻的图像与
相邻的图像与![]() 轴的一个交点.
轴的一个交点.
⑴ 求函数![]() 的解析式;
的解析式;
⑵ 若将函数![]() 的图像沿
的图像沿![]() 轴向右平移
轴向右平移![]() 个单位,再把所得图像上每一点的横坐标都变为原来的
个单位,再把所得图像上每一点的横坐标都变为原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图像,求函数
的图像,求函数![]() 的单调递增区间.
的单调递增区间.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据以往经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间的用氧量为
(米/单位时间),每单位时间的用氧量为![]() (升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为
(升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为![]() (米/单位时间),每单位时间用氧量为1.5(升),记该潜水员在此次考察活动中的总用氧量为
(米/单位时间),每单位时间用氧量为1.5(升),记该潜水员在此次考察活动中的总用氧量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求当下潜速度
,求当下潜速度![]() 取什么值时,总用氧量最少.
取什么值时,总用氧量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
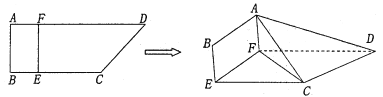
【题目】如图,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别在
分别在![]() 上,
上, ![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使
折起,使![]() .
.
(1)若![]() ,在折叠后的线段
,在折叠后的线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(2)求三棱锥![]() 的体积的最大值,并求出此时点
的体积的最大值,并求出此时点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论: ①函数 ![]() 的值域是(0,+∞);
的值域是(0,+∞);
②直线2x+ay﹣1=0与直线(a﹣1)x﹣ay﹣1=0平行,则a=﹣1;
③过点A(1,2)且在坐标轴上的截距相等的直线的方程为x+y=3;
④若圆柱的底面直径与高都等于球的直径,则圆柱的侧面积等于球的表面积.
其中正确的结论序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=4sinωxsin(ωx+ ![]() )﹣1(ω>0),f(x)的最小正周期为π. (Ⅰ)当x∈[0,
)﹣1(ω>0),f(x)的最小正周期为π. (Ⅰ)当x∈[0, ![]() ]时,求f(x)的最大值;
]时,求f(x)的最大值;
(Ⅱ)请用“五点作图法”画出f(x)在[0,π]上的图象.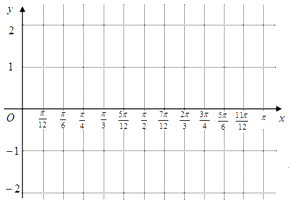
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且以原点为圆心,椭圆的焦距为直径的圆与直线
,且以原点为圆心,椭圆的焦距为直径的圆与直线![]() 相切(
相切(![]() 为常数).
为常数).

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)如图,若椭圆的![]() 左、右焦点分别为
左、右焦点分别为![]() ,过
,过![]() 作直线
作直线![]() 与椭圆分别交于两点
与椭圆分别交于两点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有长分别为1m、2m、3m的钢管各3根(每根钢管质地均匀、粗细相同附有不同的编号),从中随机抽取2根(假设各钢管被抽取的可能性是均等的),再将抽取的钢管相接焊成笔直的一根.若X表示新焊成的钢管的长度(焊接误差不计).
(1)求X的分布列;
(2)若Y=﹣λ2X+λ+1,E(Y)>1,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若满足①
,若满足①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() ,且
,且![]() 时,
时, ![]() ,则称
,则称![]() 为“偏对称函数”.现给出四个函数:
为“偏对称函数”.现给出四个函数:
①![]() ; ②
; ② 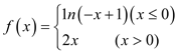 ;
;
③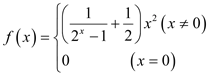 ; ④
; ④![]() .
.
则其中是“偏对称函数”的函数为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com