
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
![]()
为了研究计算的方便,工作人员将上表的数据进行了处理,![]() 得到下表2:
得到下表2:
![]()
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)通过(1)中的方程,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)用所求回归方程预测到2010年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中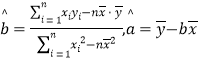 )
)
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=n2+2n;数列{bn}是公比大于1的等比数列,且满足b1+b4=9,b2b3=8.
(Ⅰ)分别求数列{an},{bn}的通项公式;
(Ⅱ)若cn=(﹣1)nSn+anbn , 求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:y2=2px(p>0)的准线与x轴交于点K,过点K作圆(x﹣5)2+y2=9的两条切线,切点为M,N,|MN|=3 ![]()
(1)求抛物线E的方程;
(2)设A,B是抛物线E上分别位于x轴两侧的两个动点,且 ![]() (其中O为坐标原点).
(其中O为坐标原点).
①求证:直线AB必过定点,并求出该定点Q的坐标;
②过点Q作AB的垂线与抛物线交于G,D两点,求四边形AGBD面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() (a>b>0)的图象是曲线C.
(a>b>0)的图象是曲线C. 
(1)在如图的坐标系中分别做出曲线C的示意图,并分别标出曲线C与x轴的左、右交点A1 , A2 .
(2)设P是曲线C上位于第一象限的任意一点,过A2作A2R⊥A1P于R,设A2R与曲线C交于Q,求直线PQ斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知3acosA=ccosB+bcosC.
(1)求cosA,sinA的值;
(2)若cosB+cosC= ![]() ,求cosC+
,求cosC+ ![]() sinC的值.
sinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:等比数列{![]() }中,公比为q,且a1=2,a4=54,等差数列{
}中,公比为q,且a1=2,a4=54,等差数列{![]() }中,公差为d,b1=2,b1+b2+b3+b4=a1+ a2+ a3.
}中,公差为d,b1=2,b1+b2+b3+b4=a1+ a2+ a3.
(I)求数列{![]() }的通项公式;
}的通项公式;
(II)求数列{![]() }的前n项和
}的前n项和![]() 的公式;
的公式;
(III)设![]() ,
,![]() ,其中n=1,2,…,试比较
,其中n=1,2,…,试比较![]() 与
与![]() 的大小,并证明你的结论.
的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某市民众对某项公共政策的态度,在该市随机抽取了![]() 名市民进行调查,做出了他们的月收入(单位:百元,范围:
名市民进行调查,做出了他们的月收入(单位:百元,范围:![]() )的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:
)的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:
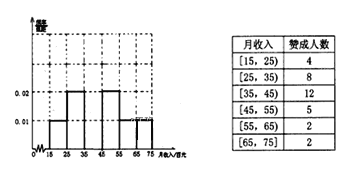
(1)求月收入在![]() 内的频率,并补全这个频率分布直方图,并在图中标出相应纵坐标;
内的频率,并补全这个频率分布直方图,并在图中标出相应纵坐标;
(2)根据频率分布直方图估计这![]() 人的平均月收入;
人的平均月收入;
(3)若从月收入(单位:百元)在![]() 的被调查者中随机选取
的被调查者中随机选取![]() 人,求
人,求![]() 人都不赞成的概率.
人都不赞成的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,有一块矩形空地ABCD,AB=2km,BC=4km,根据周边环境及地形实际,当地政府规划在该空地内建一个筝形商业区AEFG,筝形的顶点A,E,F,G为商业区的四个入口,其中入口F在边BC上(不包含顶点),入口E,G分别在边AB,AD上,且满足点A,F恰好关于直线EG对称,矩形内筝形外的区域均为绿化区. 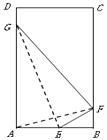
(1)请确定入口F的选址范围;
(2)设商业区的面积为S1 , 绿化区的面积为S2 , 商业区的环境舒适度指数为 ![]() ,则入口F如何选址可使得该商业区的环境舒适度指数最大?
,则入口F如何选址可使得该商业区的环境舒适度指数最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com