
【题目】如图1,直线![]() 将矩形纸
将矩形纸![]() 分为两个直角梯形
分为两个直角梯形![]() 和
和![]() ,将梯形
,将梯形![]() 沿边
沿边![]() 翻折,如图2,在翻折的过程中(平面
翻折,如图2,在翻折的过程中(平面![]() 和平面
和平面![]() 不重合),下面说法正确的是
不重合),下面说法正确的是
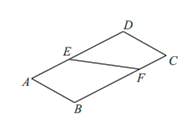
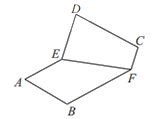
图1 图2
A.存在某一位置,使得![]() 平面
平面![]()
B.存在某一位置,使得![]() 平面
平面![]()
C.在翻折的过程中,![]() 平面
平面![]() 恒成立
恒成立
D.在翻折的过程中,![]() 平面
平面![]() 恒成立
恒成立
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】赵爽是我国古代数学家、天文学家,大约公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,又称“赵爽弦图”(以弦为边长得到的正方形是由![]() 个全等的直角三角形再加上中间的一个小正方形组成的,如图(1)),类比“赵爽弦图”,可类似地构造如图(2)所示的图形,它是由
个全等的直角三角形再加上中间的一个小正方形组成的,如图(1)),类比“赵爽弦图”,可类似地构造如图(2)所示的图形,它是由![]() 个全等的三角形与中间的一个小正六边形组成的一个大正六边形,设
个全等的三角形与中间的一个小正六边形组成的一个大正六边形,设![]() ,若在大正六边形中随机取一点,则此点取自小正六边形的概率为( )
,若在大正六边形中随机取一点,则此点取自小正六边形的概率为( )
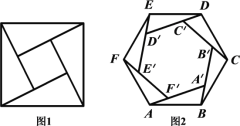
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乡镇为了发展旅游行业,决定加强宣传,据统计,广告支出费![]() 与旅游收入
与旅游收入![]() (单位:万元)之间有如下表对应数据:
(单位:万元)之间有如下表对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)求旅游收入![]() 对广告支出费
对广告支出费![]() 的线性回归方程
的线性回归方程![]() ,若广告支出费
,若广告支出费![]() 万元,预测旅游收入;
万元,预测旅游收入;
(2)在已有的五组数据中任意抽取两组,根据(1)中的线性回归方程,求至少有一组数据,其预测值与实际值之差的绝对值不超过![]() 的概率.(参考公式:
的概率.(参考公式: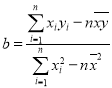 ,
,![]() ,其中
,其中![]() 为样本平均值,参考数据:
为样本平均值,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥PABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
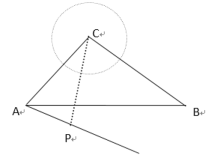
【题目】某工厂C发生爆炸出现毒气泄漏,已知毒气以圆形向外扩散,且半径以每分钟![]() 的速度增大. 一所学校A,位于工厂C南偏西
的速度增大. 一所学校A,位于工厂C南偏西![]() ,且与工厂相距
,且与工厂相距![]() .消防站B位于学校A的正东方向,且位于工厂C南偏东
.消防站B位于学校A的正东方向,且位于工厂C南偏东![]() ,立即以每分钟
,立即以每分钟![]() 的速度沿直线
的速度沿直线![]() 赶往工厂C救援,同时学校组织学生P从A处沿着南偏东
赶往工厂C救援,同时学校组织学生P从A处沿着南偏东![]() 的道路,以每分钟
的道路,以每分钟![]() 的速度进行安全疏散(与爆炸的时间差忽略不计).要想在消防员赶往工厂的时间内(包括消防员到达工厂的时刻),保证学生的安全,学生撤离的速度应满足什么要求?
的速度进行安全疏散(与爆炸的时间差忽略不计).要想在消防员赶往工厂的时间内(包括消防员到达工厂的时刻),保证学生的安全,学生撤离的速度应满足什么要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若满足①
,若满足①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() ,且
,且![]() 时,都有
时,都有![]() ,则称
,则称![]() 为“偏对称函数”.现给出四个函数:
为“偏对称函数”.现给出四个函数:![]() ;
;![]() ;
;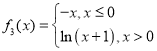 ;
;![]() .则其中是“偏对称函数”的函数个数为( )
.则其中是“偏对称函数”的函数个数为( )
A.3B.2C.1D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com