解:(1)∵
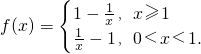
∴f(x)在(0,1)上为减函数,在(1,+∞)上是增函数.
由0<a<b,且f(a)=f(b),
可得 0<a<1<b且
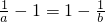
.
所以
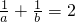
.
(2)不存在满足条件的实数a,b.
若存在满足条件的实数a,b,则0<a<b
①当a,b∈(0,1)时,
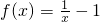
在(0,1)上为减函数.
故
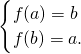
即

解得 a=b.
故此时不存在适合条件的实数a,b.
②当a,b∈[1,+∞)时,
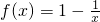
在(1,+∞)上是增函数.
故
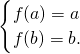
即
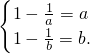
此时a,b是方程x
2-x+1=0的根,此方程无实根.
故此时不存在适合条件的实数a,b.
当a∈(0,1),b∈[1,+∞)时,由于1∈[a,b],而f(1)=0∉[a,b],
故此时不存在适合条件的实数a,b.
综上可知,不存在适合条件的实数a,b.
(3)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb].
则a>0,m>0.
当此时得a,b异号,不符合题意,所以a,b不存在.
a,b∈(0,1)时,由于f(x)在(0,1)上是减函数,
故
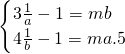
当a∈(0,1),b∈[1,+∞)时,易知0在值域内,值域不可能是[ma,mb],
所以a,b不存在.
故只有a,b∈[1,+∞)
∵f(x)在[1,+∞)上是增函数,
∴
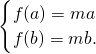
即
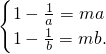
1,b是方程mx
2-x+1=0的两个根.
即关于x的方程mx
2-x+1=0有两个大于1的实根.设这两个根为x
1,x
2.
则x
1+x
2=

,x
1•x
2=

.
∴
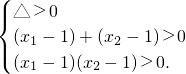
即
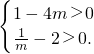
解得

.
故m的取值范围是

.
分析:(1)根据分段函数,可知f(x)在(0,1)上为减函数,在(1,+∞)上是增函数.利用f(a)=f(b),可求

的值;
(2)假设存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],分三种情况讨论:a,b∈(0,1);a,b∈[1,+∞);a∈(0,1),b∈[1,+∞),分别利用相应函数解析式求解即可;
(3)与(2)同样思路:分三种情况讨论:a,b∈(0,1);a,b∈[1,+∞);a∈(0,1),b∈[1,+∞),分别利用相应函数解析式求解即可的结论.
点评:本题的考点是函数与方程的综合应用,主要考查已知分段函数,研究函数的定义域与值域,利用方程的思想解决函数问题,有一定的难度.

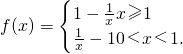
 的值;
的值;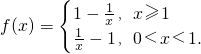
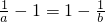 .
.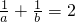 .
.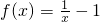 在(0,1)上为减函数.
在(0,1)上为减函数.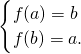 即
即 
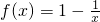 在(1,+∞)上是增函数.
在(1,+∞)上是增函数.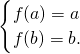
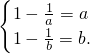
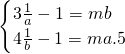
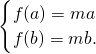 即
即 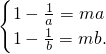
 ,x1•x2=
,x1•x2= .
.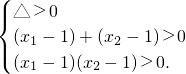
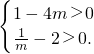
 .
.  .
. 的值;
的值;

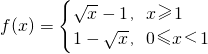
 的值;
的值;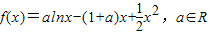
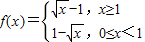
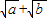 的值;
的值;