
【题目】为践行“绿水青山就是金山银山”的国家发展战略,我市对某辖区内畜牧、化工、煤炭三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到85分及其以上的单位被称为“![]() 类”环保单位,未达到85分的单位被称为“
类”环保单位,未达到85分的单位被称为“![]() 类”环保单位.现通过分层抽样的方法确定了这三类行业共20个单位进行调研,统计考评分数如下:
类”环保单位.现通过分层抽样的方法确定了这三类行业共20个单位进行调研,统计考评分数如下:
畜牧类行业:85,92,77,81,89,87
化工类行业:79,77,90,85,83,91
煤炭类行业:87,89,76,84,75,94,90,88
(1)计算该辖区这三类行业中每类行业的单位个数;
(2)若从畜牧类行业这六个单位中,再随机选取两个单位进行生产效益调查,求选出的这两个单位中既有“![]() 类”环保单位,又有“
类”环保单位,又有“![]() 类”环保单位的概率.
类”环保单位的概率.
【答案】(1)60、60、80;(2)![]()
【解析】
(1)求出三类行业的个数之比,结合分层抽样的定义可求出每类行业的单位个数.
(2)列举出六个单位中随机抽取两个所有的组合情况,即可得到总的事件个数及既有“![]() 类”环保单位,又有“
类”环保单位,又有“![]() 类”环保单位的组合个数,结合古典概型即可求概率.
类”环保单位的组合个数,结合古典概型即可求概率.
解:(1)由题意得,抽取的畜牧、化工、煤炭三类行业单位个数之比为![]() .
.
由分层抽样的定义,有畜牧类行业的单位个数为![]() ,
,
化工类行业的单位个数为![]() ,煤炭类行业的单位个数为
,煤炭类行业的单位个数为![]() ,
,
故该辖区畜牧、化工、煤炭三类行业中每类行业的单位个数分别为60、60、80.
(2)记选出的这2个单位中既有“![]() 类”环保单位,又有“
类”环保单位,又有“![]() ”环保单位为事件
”环保单位为事件![]() .这2个单位的考核数据情形有
.这2个单位的考核数据情形有
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共15种.
共15种.
其中符合的事件![]() 的考核数据情形有
的考核数据情形有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共8种,故所求概率
共8种,故所求概率![]() .
.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】为迎接“五一”节的到来,某单位举行“庆五一,展风采”的活动.现有6人参加其中的一个节目,该节目由![]() 两个环节可供参加者选择,为增加趣味性,该单位用电脑制作了一个选择方案:按下电脑键盘“Enter”键则会出现模拟抛两枚质地均匀骰子的画面,若干秒后在屏幕上出现两个点数
两个环节可供参加者选择,为增加趣味性,该单位用电脑制作了一个选择方案:按下电脑键盘“Enter”键则会出现模拟抛两枚质地均匀骰子的画面,若干秒后在屏幕上出现两个点数![]() 和
和![]() ,并在屏幕的下方计算出
,并在屏幕的下方计算出![]() 的值.现规定:每个人去按“Enter”键,当显示出来的
的值.现规定:每个人去按“Enter”键,当显示出来的![]() 小于
小于![]() 时则参加
时则参加![]() 环节,否则参加
环节,否则参加![]() 环节.
环节.
(1)求这6人中恰有2人参加该节目![]() 环节的概率;
环节的概率;
(2)用![]() 分别表示这6个人中去参加该节目
分别表示这6个人中去参加该节目![]() 两个环节的人数,记
两个环节的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】出版商为了解某科普书一个季度的销售量![]() (单位:千本)和利润
(单位:千本)和利润![]() (单位:元/本)之间的关系,对近年来几次调价之后的季销售量进行统计分析,得到如下的10组数据.
(单位:元/本)之间的关系,对近年来几次调价之后的季销售量进行统计分析,得到如下的10组数据.
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2.4 | 3.1 | 4.6 | 5.3 | 6.4 | 7.1 | 7.8 | 8.8 | 9.5 | 10 |
| 18.1 | 14.1 | 9.1 | 7.1 | 4.8 | 3.8 | 3.2 | 2.3 | 2.1 | 1.4 |
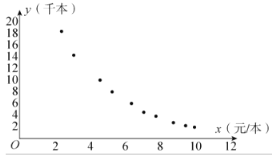
根据上述数据画出如图所示的散点图:
(1)根据图中所示的散点图判断![]() 和
和![]() 哪个更适宜作为销售量
哪个更适宜作为销售量![]() 关于利润
关于利润![]() 的回归方程类型?(给出判断即可,不需要说明理由)
的回归方程类型?(给出判断即可,不需要说明理由)
(2)根据(1)中的判断结果及参考数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)根据回归方程设该科普书一个季度的利润总额为![]() (单位:千元),当季销售量
(单位:千元),当季销售量![]() 为何值时,该书一个季度的利润总额预报值最大?(季利润总额=季销售量×每本书的利润)
为何值时,该书一个季度的利润总额预报值最大?(季利润总额=季销售量×每本书的利润)
参考公式及参考数据:
①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的公式分别为
的斜率和截距的公式分别为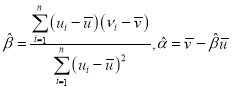 .
.
②参考数据:
|
|
|
|
|
|
|
6.50 | 6.60 | 1.75 | 82.50 | 2.70 |
|
|
表中![]() .另:
.另:![]() .计算时,所有的小数都精确到0.01.
.计算时,所有的小数都精确到0.01.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在单位正方体![]() 中,点P在线段
中,点P在线段![]() 上运动,给出以下四个命题:
上运动,给出以下四个命题:

![]() 异面直线
异面直线![]() 与
与![]() 间的距离为定值;
间的距离为定值;
![]() 三棱锥
三棱锥![]() 的体积为定值;
的体积为定值;
![]() 异面直线
异面直线![]() 与直线
与直线![]() 所成的角为定值;
所成的角为定值;
![]() 二面角
二面角![]() 的大小为定值.
的大小为定值.
其中真命题有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对所有高校学生进行普通话水平测试,发现成绩服从正态分布N(μ,σ2),下表用茎叶图列举出来抽样出的10名学生的成绩.

(1)计算这10名学生的成绩的均值和方差;
(2)给出正态分布的数据:P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9544.
由(1)估计从全市随机抽取一名学生的成绩在(76,97)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】青岛二中学生民议会在周五下午高峰时段,对公交![]() 路甲站和
路甲站和![]() 线乙站各随机抽取了
线乙站各随机抽取了![]() 位乘客,统计其乘车等待时间(指乘客从等车到乘上车的时间,乘车等待时间不超过
位乘客,统计其乘车等待时间(指乘客从等车到乘上车的时间,乘车等待时间不超过![]() 分钟).将统计数据按
分钟).将统计数据按![]() ,
,![]() ,
,![]() ,…,
,…,![]() 分组,制成频率分布直方图:
分组,制成频率分布直方图:

假设乘客乘车等待时间相互独立.
(1)此时段,从甲站的乘客中随机抽取![]() 人,记为事件
人,记为事件![]() ;从乙站的乘客中随机抽取
;从乙站的乘客中随机抽取![]() 人,记为事件
人,记为事件![]() .若用频率估计概率,求“两人乘车等待时间都小于
.若用频率估计概率,求“两人乘车等待时间都小于![]() 分钟”的概率;
分钟”的概率;
(2)此时段,从乙站![]() 的乘客中随机抽取
的乘客中随机抽取![]() 人(不重复抽取),抽得在
人(不重复抽取),抽得在![]() 的人数为
的人数为![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某两名高三学生连续9次数学测试的成绩(单位:分)进行统计得到如下折线图.下列有关这两名学生数学成绩的分析中,正确的结论是( )
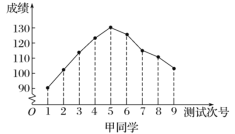

A.甲同学的成绩折线图具有较好的对称性,与正态曲线相近,故而平均成绩为130分
B.根据甲同学成绩折线图中的数据进行统计,估计该同学平均成绩在区间![]() 内
内
C.乙同学的数学成绩与测试次号具有比较明显的线性相关性,且为正相关
D.乙同学在这连续九次测验中的最高分与最低分的差超过40分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:指数函数![]() 在R上是单调减函数;命题q:关于x的方程
在R上是单调减函数;命题q:关于x的方程![]() 有实根,
有实根,
(1)若p为真,求a的范围
(2)若q为真,求![]() 的范围
的范围
(3)若p或q为真,p且q为假,求实数a的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com