
【题目】若函数![]() 的图象上存在两个不同的点
的图象上存在两个不同的点![]() 、
、![]() ,使得曲线
,使得曲线![]() 在这两点处的切线重合,称函数
在这两点处的切线重合,称函数![]() 具有
具有![]() 性质.下列函数中具有
性质.下列函数中具有![]() 性质的有( )
性质的有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】BD
【解析】
根据题意可知性质![]() 指函数
指函数![]() 的图象上有两个不同点的切线是重合的,分析各选项中函数的导函数的单调性与原函数的奇偶性,数形结合可判断A、B选项的正误;利用导数相等,求解方程,可判断C、D选项的正误.综合可得出结论.
的图象上有两个不同点的切线是重合的,分析各选项中函数的导函数的单调性与原函数的奇偶性,数形结合可判断A、B选项的正误;利用导数相等,求解方程,可判断C、D选项的正误.综合可得出结论.
由题意可得,性质![]() 指函数
指函数![]() 的图象上有两个不同点的切线是重合的,即两个不同点所对应的导数值相等,且该点处函数的切线方程也相等.
的图象上有两个不同点的切线是重合的,即两个不同点所对应的导数值相等,且该点处函数的切线方程也相等.
对于A选项,![]() ,则
,则![]() ,导函数为增函数,不存在不同的两个
,导函数为增函数,不存在不同的两个![]() 使得导数值相等,所以A不符合;
使得导数值相等,所以A不符合;
对于B选项,函数![]() 为偶函数,
为偶函数,![]() ,
,
令![]() ,可得
,可得![]() 或
或![]() ,如下图所示:
,如下图所示:
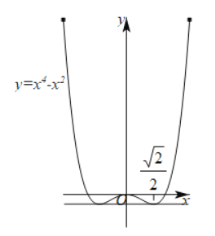
由图象可知,函数![]() 在
在![]() 和
和![]() 处的切线重合,所以B选项符合;
处的切线重合,所以B选项符合;
对于C选项,设两切点分别为![]() 和
和![]() ,则两切点处的导数值相等有:
,则两切点处的导数值相等有:![]() ,解得:
,解得:![]() ,令
,令![]() ,则
,则![]() ,
,
两切点处的导数![]() ,两切点连线的斜率为
,两切点连线的斜率为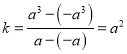 ,则
,则![]() ,得
,得![]() ,两切点重合,不符合题意,所以C选项不符合;
,两切点重合,不符合题意,所以C选项不符合;
对于D选项,![]() ,设两切点得横坐标分别为
,设两切点得横坐标分别为![]() 和
和![]() ,
,
则![]() ,所以
,所以![]() ,
,
取![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
两切点处的导数值为![]() ,两切点连线的直线斜率为
,两切点连线的直线斜率为![]() ,
,
所以两切点处的导数值等于两切点连线的斜率,符合性质![]() ,所以D选项符合.
,所以D选项符合.
故选:BD.


科目:高中数学 来源: 题型:
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,现从高一学生中抽取![]() 人做调查,得到
人做调查,得到![]() 列联表:
列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 100 |
且已知在![]() 个人中随机抽取
个人中随机抽取![]() 人,抽到喜欢游泳的学生的概率为
人,抽到喜欢游泳的学生的概率为![]() .
.
(1)请完成上面的列联表;
(2)根据列联表的数据,是否有![]() 的把握认为喜欢游泳与性别有关?并说明你的理由.
的把握认为喜欢游泳与性别有关?并说明你的理由.
附: (其中
(其中![]() )和临界值表:
)和临界值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.45 | 0.708 | 1.32 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年中央电视台在周日晚上推出的一档新的综艺节目,为了解节目效果,一次节目结束后,现随机抽取了
年中央电视台在周日晚上推出的一档新的综艺节目,为了解节目效果,一次节目结束后,现随机抽取了![]() 名观众(含
名观众(含![]() 名女性)的评分(百分制)进行分析,分别得到如图所示的两个频率分布直方图.
名女性)的评分(百分制)进行分析,分别得到如图所示的两个频率分布直方图.

(1)计算女性观众评分的中位数与男性观众评分的平均分;
(2)若把评分低于![]() 分定为“不满意”,评分不低于
分定为“不满意”,评分不低于![]() 分定为“满意”.
分定为“满意”.
(i)试比较男观众与女观众不满意的概率大小,并说明理由;
(ii)完成下列![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为性别和对该综艺节目是否满意有关.
的把握认为性别和对该综艺节目是否满意有关.
女性观众 | 男性观众 | 合计 | |
“满意” | |||
“不满意” | |||
合计 |
参考数据:
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数的极值;
垂直,求函数的极值;
(2)设函数![]() .当
.当![]() =
=![]() 时,若区间[1,e]上存在x0,使得
时,若区间[1,e]上存在x0,使得![]() ,求实数
,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数底数)
为自然对数底数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com