
设函数f(x)=x3-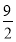 x2+6x-a.
x2+6x-a.
(1)对于任意实数x,f′(x)≥m恒成立,求m的最大值;
(2)若方程f(x)=0有且仅有一个实根,求a的取值范围.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(解析版) 题型:选择题
如图所示,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是 ( ).

A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-3-2练习卷(解析版) 题型:填空题
已知△ABC的三边长成公比为 的等比数列,则其最大角的余弦值为________.
的等比数列,则其最大角的余弦值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(解析版) 题型:解答题
已知函数f(x)=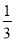 x3+
x3+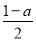 x2-ax-a,x∈R,其中a>0.
x2-ax-a,x∈R,其中a>0.
(1)求函数f(x)的单调区间;
(2)若函数f(x)在区间(-2,0)内恰有两个零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(解析版) 题型:选择题
设函数f(x)=ax2+bx+c(a,b,c∈R),若x=-1为函数f(x)ex的一个极值点,则下列图象不可能为y=f(x)的图象是( ).

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-2练习卷(解析版) 题型:选择题
设函数f(x)=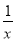 ,g(x)=-x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是 ( ).
,g(x)=-x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是 ( ).
A.x1+x2>0,y1+y2>0
B.x1+x2<0,y1+y2>0
C.x1+x2>0,y1+y2<0
D.x1+x2<0,y1+y2<0
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-1练习卷(解析版) 题型:解答题
已知奇函数f(x)在定义域[-2,2]上单调递减,求满足f(1-m)+f(1-m2)<0的实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-1-3练习卷(解析版) 题型:选择题
小王从甲地到乙地往返的时速分别为a和b(a<b),其全程的平均时速为v,则( ).
A.a<v< 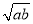 B.v=
B.v=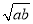
C. 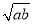 <v<
<v< 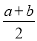 D.v=
D.v=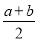
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com