
【题目】某甲![]() 篮球队的12名队员(含2名外援)中有5名主力队员(含一名外援),主教练要从12名队员中选5人首发上场,则主力队员不少于4人,且有一名外援上场的概率是_____.
篮球队的12名队员(含2名外援)中有5名主力队员(含一名外援),主教练要从12名队员中选5人首发上场,则主力队员不少于4人,且有一名外援上场的概率是_____.
【答案】![]()
【解析】
由题意可得:基本事件总数为![]() ,主力队员不少于4人,即5名队员中有主力队员4人或者5人,并且其选法分别为
,主力队员不少于4人,即5名队员中有主力队员4人或者5人,并且其选法分别为![]() 种、1种,进而根据等可能事件的概率公式可得答案.
种、1种,进而根据等可能事件的概率公式可得答案.
由题意可得:主教练要从12名队员中选5人首发上场不同的选法有:![]() 种.
种.
因为主力队员不少于4人,所以5名队员中有主力队员4人或者5人,
当从12名队员中选5人首发上场其中主力队员为4人并且有一名外援上场时,不同的选法共有![]() 种;
种;
当从12名队员中选5人首发上场其中主力队员为5人并且有一名外援上场时,不同的选法共有1种,
所以主力队员不少于4人,且有一名外援上场的选法共有26种,
所以主力队员不少于4人,且有一名外援上场的概率为:![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.
的上界.
(1)设![]() ,判断
,判断![]() 在
在![]() 上是否为有界函数,若是,请说明理由,并写出
上是否为有界函数,若是,请说明理由,并写出![]() 的所有上界
的所有上界![]() 的集合;若不是,也请说明理由;
的集合;若不是,也请说明理由;
(2)若函数![]() 在
在![]() 上是以
上是以![]() 为上界的有界函数,求实数
为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知非空集合![]() 是由一些函数组成,满足如下性质:①对任意
是由一些函数组成,满足如下性质:①对任意![]() ,
,![]() 均存在反函数
均存在反函数![]() ,且
,且![]() ;②对任意
;②对任意![]() ,方程
,方程![]() 均有解;③对任意
均有解;③对任意![]() 、
、![]() ,若函数
,若函数![]() 为定义在
为定义在![]() 上的一次函数,则
上的一次函数,则![]() .
.
(1)若![]() ,
,![]() ,均在集合
,均在集合![]() 中,求证:函数
中,求证:函数![]() ;
;
(2)若函数![]() (
(![]() )在集合
)在集合![]() 中,求实数
中,求实数![]() 的取值范围;
的取值范围;
(3)若集合![]() 中的函数均为定义在
中的函数均为定义在![]() 上的一次函数,求证:存在一个实数
上的一次函数,求证:存在一个实数![]() ,使得对一切
,使得对一切![]() ,均有
,均有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个不相等的非零向量![]() ,两组向量
,两组向量![]() 和
和![]() 均由2个
均由2个![]() 和3个
和3个![]() 排列而成,记
排列而成,记![]() ,
,![]() 表示
表示![]() 所有可能取值中的最小值,则下列命题中
所有可能取值中的最小值,则下列命题中
(1)![]() 有5个不同的值;(2)若
有5个不同的值;(2)若![]() 则
则![]() 与
与![]() 无关;(3)若
无关;(3)若![]() ,则
,则![]() 与
与![]() 无关;(4)若
无关;(4)若![]() ,则
,则![]() ;(5)若
;(5)若![]() ,
,![]() ,则
,则![]() 与
与![]() 的夹角为
的夹角为![]() .正确的是( )
.正确的是( )
A.(1)(2)B.(2)(4)C.(3)(5)D.(1)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了配合今年上海迪斯尼乐园工作,某单位设计了统计人数的数学模型![]() ,以
,以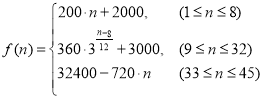 表示第
表示第![]() 个时刻进入园区的人数;以
个时刻进入园区的人数;以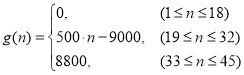 表示第
表示第![]() 个时刻离开园区的人数.设定以15分钟为一个计算单位,上午9点15分作为第1个计算人数单位,即
个时刻离开园区的人数.设定以15分钟为一个计算单位,上午9点15分作为第1个计算人数单位,即![]() ;9点30分作为第2个计算单位,即
;9点30分作为第2个计算单位,即![]() ;依次类推,把一天内从上午9点到晚上8点15分分成45个计算单位(最后结果四舍五入,精确到整数).
;依次类推,把一天内从上午9点到晚上8点15分分成45个计算单位(最后结果四舍五入,精确到整数).
(1)试计算当天14点至15点这1小时内进入园区的游客人数![]() 、离开园区的游客人数
、离开园区的游客人数![]()
![]() 各为多少?
各为多少?
(2)从13点45分(即![]() )开始,有游客离开园区,请你求出这之后的园区内游客总人数最多的时刻,并说明理由.
)开始,有游客离开园区,请你求出这之后的园区内游客总人数最多的时刻,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一研学实践活动小组利用课余时间,对某公司1月份至5月份销售某种产品的销售量及销售单价进行了调查,月销售单价![]() (单位:元)和月销售量
(单位:元)和月销售量![]() (单位:百件)之间的一组数据如下表所示:
(单位:百件)之间的一组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 |
月销售单价 | 1.6 | 1.8 | 2 | 2.2 | 2.4 |
月销售量 | 10 | 8 | 7 | 6 | 4 |
(1)根据1至5月份的数据,求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)预计在今后的销售中,月销售量与月销售单价仍然服从(1)中的关系,若该种产品的成本是1元/件,那么该产品的月销售单价应定为多少元才能获得最大月利润?(注:利润=销售收入-成本)
(回归直线方程![]() ,其中
,其中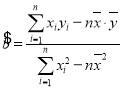 .参考数据:
.参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列![]() ,
,![]() ,若
,若![]() -
-![]()
![]() …,则称
…,则称![]() 是
是![]() 的“收缩数列”.其中,
的“收缩数列”.其中,![]() ,
,![]() 分别表示
分别表示![]() 中的最大数和最小数.已知
中的最大数和最小数.已知![]() 为无穷数列,其前
为无穷数列,其前![]() 项和为
项和为![]() ,数列
,数列![]() 是
是![]() 的“收缩数列”.
的“收缩数列”.
(1)若![]() ,求
,求![]() 的前
的前![]() 项和;
项和;
(2)证明:![]() 的“收缩数列”仍是
的“收缩数列”仍是![]() ;
;
(3)若![]() ,求所有满足该条件的
,求所有满足该条件的![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三角形ABE与菱形ABCD所在的平面互相垂直,![]() ,
,![]() ,M是AB的中点.
,M是AB的中点.
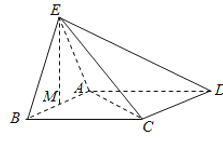
(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在线段EC上是否存在点P,使得直线AP与平面ABE所成的角为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com