
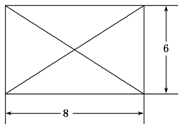
 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.分析 (Ⅰ)由三视图知该几何体是一个底面为矩形,高为4,顶点在底面的射影是底面中心的四棱锥,由此能求出该几何体的体积.
(Ⅱ)该四棱锥有两个侧面是全等的等腰三角形,另外两个侧面也是全等的等腰三角形,由此能求出该几何体的面积.
解答 解:(Ⅰ)由三视图知该几何体是一个底面为矩形,高为4,顶点在底面的射影是底面中心的四棱锥,
∴该几何体的体积V=$\frac{1}{3}×(8×6)×4$=64.
(Ⅱ)该四棱锥有两个侧面是全等的等腰三角形,且其高为h1=$\sqrt{{4}^{2}+(\frac{8}{2})^{2}}$=4$\sqrt{2}$,
另外两个侧面也是全等的等腰三角形,这两个侧面的高为${{h}_{2}}^{\;}$=$\sqrt{{4}^{2}+(\frac{6}{2})^{2}}$=5,
∴该几何体的面积S=2($\frac{1}{2}×6×4\sqrt{2}+\frac{1}{2}×8×5$)+8×6=88+24$\sqrt{2}$.
点评 本题考查几何体的体积和面积的求法,是基础题,解题时要认真审题,注意三视图的性质的合理运用.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题p:“?x∈R,sin x+cos x=$\sqrt{2}$”,则非P是真命题 | |
| B. | “a>1”是“f(x)=logax(a>0,且a≠1)在(0,+∞)上为增函数”的充要条件 | |
| C. | 命题“?x∈R,$\sqrt{x+1}$>x”的否定是真命题 | |
| D. | “x=-1”是“x2-5x-6=0”的必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -30 | B. | 15 | C. | -60 | D. | -15 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
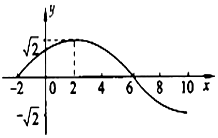 若函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数的单调增区间为[16k-6,16k+2],k∈Z.
若函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数的单调增区间为[16k-6,16k+2],k∈Z.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com