
【题目】已知函数f(x)=1-![]() (a>0且a≠1)是定义在(-∞,+∞)上的奇函数.
(a>0且a≠1)是定义在(-∞,+∞)上的奇函数.
(1)求a的值;
(2)证明:函数f(x)在定义域(-∞,+∞)内是增函数;
(3)当x∈(0,1]时,tf(x)≥2x-2恒成立,求实数t的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某厂为检验车间一生产线是否工作正常,现从生产线中随机抽取一批零件样本,测量尺寸(单位: mm )绘成频率分布直方图如图所示:
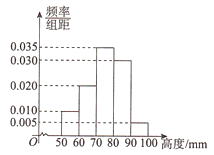
(Ⅰ)求该批零件样本尺寸的平均数 x 和样本方差 ![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)若该批零件尺寸![]() 服从正态分布
服从正态分布 ![]() ,其中
,其中 ![]() 近似为样本平均数
近似为样本平均数 ![]() 近似为样本方差
近似为样本方差 ![]() ,利用该正态分布求
,利用该正态分布求 ![]() ;
;
(Ⅲ)若从生产线中任取一零件,测量尺寸为30mm,根据 ![]() 原则判断该生产线是否正常?
原则判断该生产线是否正常?
附: ![]() ;若
;若![]() ,则
,则 ![]() ,
, ![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
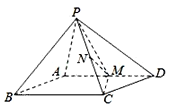
【题目】如图,已知四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥平面ABCD.M是AD的中点,N是PC的中点.
(1)求证:MN∥平面PAB;
(2)若平面PMC⊥平面PAD,求证:CM⊥AD;
(3)若平面ABCD是矩形,PA=AB,求证:平面PMC⊥平面PBC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据市场调查发现,某种产品在投放市场的30天中,其销售价格![]() (元)和时间
(元)和时间![]() (天)的关系如图所示.
(天)的关系如图所示.

(1)求销售价格![]() (元)和时间
(元)和时间![]() (天)的函数关系式;
(天)的函数关系式;
(2)若日销售量![]() (件)与时间
(件)与时间![]() (天)的函数关系式是
(天)的函数关系式是![]()
![]() ,问该产品投放市场第几天时,日销售额
,问该产品投放市场第几天时,日销售额![]() (元)最高,且最高为多少元?
(元)最高,且最高为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( ) 
A.y= ![]() ﹣
﹣ ![]() x
x
B.y= ![]() x3﹣
x3﹣ ![]() x
x
C.y= ![]() x3﹣x
x3﹣x
D.y=﹣ ![]() x3+
x3+ ![]() x
x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某单位职工的月收入情况画出的样本频率分布直方图,已知图中第一组的频数为4 000,请根据该图提供的信息,解答下列问题.
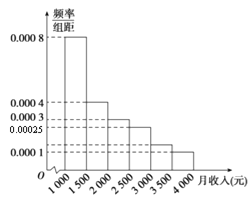
(1)为了分析职工的收入与年龄、学历等方面的关系,必须从样本中按月收入用分层抽样方法抽出100人作进一步分析,则月收入在[1 500,2 000)的这组中应抽取多少人?
(2)试估计样本数据的中位数与平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com