
平面直角坐标系xoy中,动点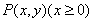 满足:点P到定点
满足:点P到定点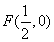 与到y轴的距离之差为
与到y轴的距离之差为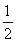 .记动点P的轨迹为曲线C.
.记动点P的轨迹为曲线C.
(1)求曲线C的轨迹方程;
(2)过点F的直线交曲线C于A、B两点,过点A和原点O的直线交直线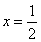 于点D,求证:直线DB平行于x轴.
于点D,求证:直线DB平行于x轴.
(1) ,(2)详见解析.
,(2)详见解析.
【解析】
试题分析:(1)求动点轨迹方程,首先设动点坐标,本题已设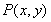 ,其次列动点满足条件
,其次列动点满足条件 ,然后利用坐标化简关系式,即
,然后利用坐标化简关系式,即 ,
, ,最后要考虑动点满足限制条件,本题为已知条件
,最后要考虑动点满足限制条件,本题为已知条件 ,另外本题对条件
,另外本题对条件 的化简也可从抛物线的定义上理解,这样更快,(2)证明直线平行于
的化简也可从抛物线的定义上理解,这样更快,(2)证明直线平行于 轴,可利用斜率为零,或证明纵坐标相等,总之都需要从坐标出发.注意到点在抛物线上,设点的坐标可简洁,设
轴,可利用斜率为零,或证明纵坐标相等,总之都需要从坐标出发.注意到点在抛物线上,设点的坐标可简洁,设 的坐标为
的坐标为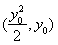 ,利用
,利用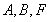 三点共线解出点
三点共线解出点 的纵坐标为
的纵坐标为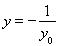 ,根据直线
,根据直线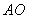 与直线
与直线 的交点解出
的交点解出 的纵坐标也为
的纵坐标也为 .
.
试题解析:(1)依题意: 2分
2分
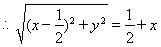
 4分
4分
 6分
6分
注:或直接用定义求解.
(2)法1:设 ,直线
,直线 的方程为
的方程为
由 得
得 8分
8分
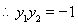
直线 的方程为
的方程为
 点
点 的坐标为
的坐标为 2分
2分

 直线
直线 平行于
平行于 轴. 14分
轴. 14分
法2:设 的坐标为
的坐标为 ,则
,则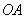 的方程为
的方程为
 点
点 的纵坐标为
的纵坐标为 , 8分
, 8分

 直线
直线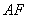 的方程为
的方程为
 点
点 的纵坐标为
的纵坐标为 . 12分
. 12分
 轴;当
轴;当 时,结论也成立,
时,结论也成立,
 直线
直线 平行于
平行于 轴. 14分
轴. 14分
考点:轨迹方程,直线与抛物线位置关系


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:高中数学 来源: 题型:
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
| n(n+1)(n+2) |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 2 |
| 3π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
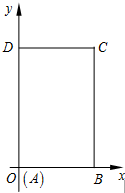 如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.
如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com