
【题目】.如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,侧棱
是正方形,侧棱![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() .
.
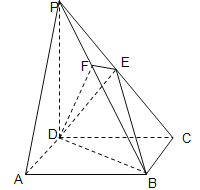
(1)证明![]() //平面
//平面![]() ;
;
(2)证明![]() ⊥平面
⊥平面![]() ;
;
(3)求![]() .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】用红、黄、蓝三种不同的颜色给大小相同的三个圆随机涂色,每个圆只涂一种颜色.设事件![]() “三个圆的颜色全不相同”,事件
“三个圆的颜色全不相同”,事件![]() “三个圆的颜色不全相同”,事件
“三个圆的颜色不全相同”,事件![]() “其中两个圆的颜色相同”,事件
“其中两个圆的颜色相同”,事件![]() “三个圆的颜色全相同”.
“三个圆的颜色全相同”.
(1)写出试验的样本空间.
(2)用集合的形式表示事件![]() .
.
(3)事件![]() 与事件
与事件![]() 有什么关系?事件
有什么关系?事件![]() 和
和![]() 的交事件与事件
的交事件与事件![]() 有什么关系?并说明理由.
有什么关系?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·江苏高考)如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.

求证:(1)EF∥平面ABC;
(2)AD⊥AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值![]() 来衡量.当
来衡量.当![]() 时,产品为一等品;当
时,产品为一等品;当![]() 时,产品为二等品;当
时,产品为二等品;当![]() 时,产品为三等品.现从甲、乙两条生产线,各随机抽取了100件该产品作为样本,测量每件产品的质量指标值,整理得到甲、乙两条生产线产品的质量指标值的频率分布直方图如图所示,视样本的频率为总体的概率.
时,产品为三等品.现从甲、乙两条生产线,各随机抽取了100件该产品作为样本,测量每件产品的质量指标值,整理得到甲、乙两条生产线产品的质量指标值的频率分布直方图如图所示,视样本的频率为总体的概率.


(1)若从甲、乙生产线生产的产品中各随机抽取1件,求恰好抽到1件一等品的概率;
(2)若一件三等品、二等品、一等品的利润分别为10元、20元、30元,从乙生产线生产的产品中随机抽取2件,求这两件产品的利润之和![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若从甲生产线生产的产品中随机抽取![]() 件,其中抽到二等品的件数为随机变量
件,其中抽到二等品的件数为随机变量![]() ,且
,且![]() 的数学期望不小于1200,求
的数学期望不小于1200,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角坐标系中,圆的方程为 为圆上三个定点,某同学从A点开始,用掷骰子的方法移动棋子,规定:①每掷一次骰子,把一枚棋子从一个定点沿圆弧移动到相邻下一个定点;②棋子移动的方向由掷骰子决定,若掷出骰子的点数为3的倍数,则按图中箭头方向移动;若掷出骰子的点数为不为3的倍数,则按图中箭头相反的方向移动.设掷骰子
为圆上三个定点,某同学从A点开始,用掷骰子的方法移动棋子,规定:①每掷一次骰子,把一枚棋子从一个定点沿圆弧移动到相邻下一个定点;②棋子移动的方向由掷骰子决定,若掷出骰子的点数为3的倍数,则按图中箭头方向移动;若掷出骰子的点数为不为3的倍数,则按图中箭头相反的方向移动.设掷骰子![]() 次时,棋子移动到A,B,C处的概率分别为
次时,棋子移动到A,B,C处的概率分别为![]() 例如:掷骰子一次时,棋子移动到A,B,C处的概率分别为
例如:掷骰子一次时,棋子移动到A,B,C处的概率分别为![]() ,
,![]() .
.

(1)分别掷骰子二次,三次时,求棋子分别移动到A,B,C处的概率;
(2)掷骰子N次时,若以X轴非负半轴为始边,以射线OA,OB,OC为终边的角的正弦值弦值记为随机变量![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com