
【题目】已知椭圆![]() 的左、右顶点分别为A,B,直线l斜率大于0,且l经过椭圆的右焦点F,与椭圆交于两点P,Q,若△AFP,△BFQ的面积分别为S1,S2,若
的左、右顶点分别为A,B,直线l斜率大于0,且l经过椭圆的右焦点F,与椭圆交于两点P,Q,若△AFP,△BFQ的面积分别为S1,S2,若![]() ,则直线l的斜率为_____.
,则直线l的斜率为_____.
科目:高中数学 来源: 题型:
【题目】椭圆: ![]() (a>b>0),左右焦点分别是F1 , F2 , 焦距为2c,若直线
(a>b>0),左右焦点分别是F1 , F2 , 焦距为2c,若直线 ![]() 与椭圆交于M点,满足∠MF1F2=2∠MF2F1 , 则离心率是( )
与椭圆交于M点,满足∠MF1F2=2∠MF2F1 , 则离心率是( )
A.![]()
B.![]() -1
-1
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R.a,b∈R,若此函数同时满足:
①当a+b=0时,有f(a)+f(b)=0;
②当a+b>0时,有f(a)+f(b)>0,
则称函数f(x)为Ω函数.
在下列函数中:
①y=x+sinx;
②y=3x﹣( ![]() )x;
)x;
③y= 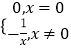
是Ω函数的为 . (填出所有符合要求的函数序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
求分数在[120,130)内的频率,并补全这个频
率分布直方图;
统计方法中,同一组数据常用该组区间的中点
值作为代表,据此估计本次考试的平均分;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段[120,130)内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的方程为x2+(y﹣2)2=1,直线l的方程为x﹣2y=0,点P在直线l上,过点P作圆M的切线PA,PB,切点为A,B.
(1)若点P的横坐标为1,求切线PA,PB的方程;
(2)若点P的纵坐标为a,且在圆M上存在点Q到点P的距离为1,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣x,若对任意x1 , x2∈[2,+∞),且x1≠x2 , 不等式 ![]() >0恒成立,则实数a的取值范围是( )
>0恒成立,则实数a的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是双曲线E:
分别是双曲线E: ![]()
![]() 的左、右焦点,P是双曲线上一点,
的左、右焦点,P是双曲线上一点, ![]() 到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当
到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当![]() 时,
时, ![]() 的面积为
的面积为![]() ,求此双曲线的方程。
,求此双曲线的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在高二年级实行选课走班教学,学校为学生提供了多种课程,其中数学科提供5种不同层次的课程,分别称为数学1、数学2、数学3、数学4、数学5,每个学生只能从这5种数学课程中选择一种学习,该校高二年级1800名学生的数学选课人数统计如表:
课程 | 数学1 | 数学2 | 数学3 | 数学4 | 数学5 | 合计 |
选课人数 | 180 | 540 | 540 | 360 | 180 | 1800 |
为了了解数学成绩与学生选课情况之间的关系,用分层抽样的方法从这1800名学生中抽取了10人进行分析.
(1)从选出的10名学生中随机抽取3人,求这3人中至少有2人选择数学2的概率;
(2)从选出的10名学生中随机抽取3人,记这3人中选择数学2的人数为X,选择数学1的人数为Y,设随机变量ξ=X﹣Y,求随机变量ξ的分布列和数学期望E(ξ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com