
【题目】已知函数![]() ,.
,.
(1)当![]() 为何值时,直线
为何值时,直线![]() 是曲线
是曲线![]() 的切线;
的切线;
(2)若不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() .(2)
.(2) ![]() .
.
【解析】
(1)先令![]() ,求其导数,设切点为
,求其导数,设切点为![]() ,由直线
,由直线![]() 是曲线
是曲线![]() 的切线,得到
的切线,得到![]() ,用导数的方法研究函数
,用导数的方法研究函数![]() 的单调性,即可求出结果;
的单调性,即可求出结果;
(2)先令![]() ,对其求导,分别讨论
,对其求导,分别讨论![]() 和
和![]() 两种情况,结合题意,即可得到结果.
两种情况,结合题意,即可得到结果.
(1)令![]() ,
,![]() ,
,
设切点为![]() ,则
,则![]() ,
,![]() ,则
,则![]() .
.
令![]() ,
,![]() ,则函数
,则函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,且
上单调递增,且![]() ,所以
,所以![]() .
.
(2)令![]() ,则
,则![]() ,
,
①当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,所以
,所以![]() 满足题意.
满足题意.
②当![]() 时,令
时,令![]() ,得
,得![]() ,
,
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(ⅰ)当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以![]() ,此时无解.
,此时无解.
(ⅱ)当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
所以![]() .
.
设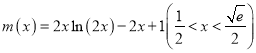 ,则
,则![]() ,
,
所以![]() 在
在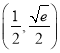 上单调递增,
上单调递增,
![]() ,不满足题意.
,不满足题意.
(ⅲ)当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,所以
,所以![]() 满足题意.
满足题意.
综上所述:![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,直线
轴的非负半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设![]() 是曲线
是曲线![]() 上的一个动眯,当
上的一个动眯,当![]() 时,求点
时,求点![]() 到直线
到直线![]() 的距离的最小值;
的距离的最小值;
(2)若曲线![]() 上所有的点都在直线
上所有的点都在直线![]() 的右下方,求实数
的右下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“割圆术”是刘徽最突出的数学成就之一,他在《九章算术注》中提出割圆术,并作为计算圆的周长,面积已经圆周率的基础,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和3.1416这两个近似数值,这个结果是当时世界上圆周率计算的最精确数据.如图,当分割到圆内接正六边形时,某同学利用计算机随机模拟法向圆内随机投掷点,计算得出该点落在正六边形内的频率为0.8269,那么通过该实验计算出来的圆周率近似值为(参考数据:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】时下,网校教学越来越受到广大学生的喜爱,它已经成为学生们课外学习的一种趋势,假设某网校的套题每日的销售量![]() (单位:千套)与销售价格
(单位:千套)与销售价格![]() (单位:元/套)满足的关系式
(单位:元/套)满足的关系式![]() ,其中
,其中![]() ,
,![]() 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套.
(1)求![]() 的值;
的值;
(2)假设网校的员工工资,办公等所有开销折合为每套题2元(只考虑销售出的套数),试确定销售价格![]() 的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查居民对城市共享单车的满意度,随机选取了100人进行问卷调查,并将问卷中的100人根据其满意度评分值按照![]() 分为5组,得到号如图所示的频率分布直方图.
分为5组,得到号如图所示的频率分布直方图.
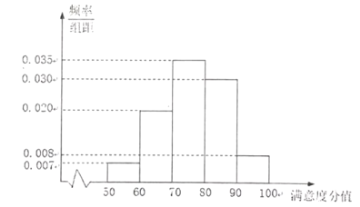
(Ⅰ)求满意度分值不低于70分的人数.
(Ⅱ)已知满意度分值在![]() 内的男性与女性的比为3:4,为提高共享单车的满意度,现从满意度分值在
内的男性与女性的比为3:4,为提高共享单车的满意度,现从满意度分值在![]() 的人中随机抽取2人进行座谈,求这2人中只有一位男性的概率.
的人中随机抽取2人进行座谈,求这2人中只有一位男性的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com