
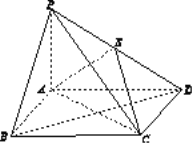
【题目】(本题满分12分)如图13,四棱锥P ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(1)证明:PB∥平面AEC;
(2)设AP=1,AD=![]() ,三棱锥P ABD的体积V=
,三棱锥P ABD的体积V=![]() ,求A到平面PBC的距离.
,求A到平面PBC的距离.
【答案】(1)略(2)![]()
【解析】试题分析:证明线面平有两种思路,一是寻求线线平行,二是寻求面面平行;已知三棱锥的体积求点到平面的距离,可借助面面垂直的性质定理根据三棱锥![]() 的体积求出
的体积求出![]() 长,由于
长,由于![]() 平面PAB,可以得出平面
平面PAB,可以得出平面![]() 平面
平面![]() ,可借助面面垂直的性质定理做出点
,可借助面面垂直的性质定理做出点![]() ,垂足为
,垂足为![]() ,可得
,可得![]() 平面
平面![]() ,即
,即![]() 的长为点
的长为点![]() 到平面
到平面![]() 的距离,再求出
的距离,再求出![]() ,这是一种传统方法.
,这是一种传统方法.
试题解析:
(1)证明:设BD与AC的交点为O,连接EO.
因为ABCD为矩形,所以O为BD的中点.
又E为PD的中点,所以EO∥PB.
EO平面AEC,PB平面AEC,
所以PB∥平面AEC.
(2)V=![]() ×
×![]() ×PA×AB×AD=
×PA×AB×AD=![]() AB,由V=
AB,由V=![]() ,可得AB=
,可得AB=![]() .
.
作AH⊥PB交PB于点H.
由题设知BC⊥平面PAB,所以BC⊥AH,因为PB∩BC=B,所以AH⊥平面PBC.
又AH=![]() =
=![]() ,
,
所以点A到平面PBC的距离为![]()


科目:高中数学 来源: 题型:
【题目】已知命题p:设a,b∈R,则“a+b>4”是“a>2且b>2”的必要不充分条件;命题q:若 ![]() <0,则
<0,则 ![]() ,
, ![]() 夹角为钝角,在命题①p∧q;②¬p∨¬q;③p∨¬q;④¬p∨q中,真命题是( )
夹角为钝角,在命题①p∧q;②¬p∨¬q;③p∨¬q;④¬p∨q中,真命题是( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品关税与市场供应量P的关系近似地满足:P(x)=2 ![]() (其中t为关税的税率,且t∈[0,
(其中t为关税的税率,且t∈[0, ![]() ],x为市场价格,b,k为正常数),当t=
],x为市场价格,b,k为正常数),当t= ![]() 时,市场供应量曲线如图所示:
时,市场供应量曲线如图所示: 
(1)根据函数图象求k,b的值;
(2)若市场需求量Q,它近似满足Q(x)=2 ![]() .当P=Q时的市场价格为均衡价格,为使均衡价格控制在不低于9元的范围内,求税率t的最小值.
.当P=Q时的市场价格为均衡价格,为使均衡价格控制在不低于9元的范围内,求税率t的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 的距离比
的距离比![]() 到定直线
到定直线![]() 的距离小1.
的距离小1.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 和
和![]() .设线段
.设线段![]() ,
, ![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 恒过一个定点;
恒过一个定点;
(Ⅲ)在(Ⅱ)的条件下,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)已知函数f(x)=2cos x(sin x+cos x).
(1)求f![]() 的值;
的值;
(2)求函数f(x)的最小正周期及单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列四个命题:
p1:若直线l和平面α内的无数条直线垂直,则l⊥α;
p2:若f(x)=2x﹣2﹣x , 则x∈R,f(﹣x)=﹣f(x);
p3:若 ![]() ,则x0∈(0,+∞),f(x0)=1;
,则x0∈(0,+∞),f(x0)=1;
p4:在△ABC中,若A>B,则sinA>sinB.
其中真命题的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某池塘中原有一块浮草,浮草蔓延后的面积y(m2)与时间t(月)之间的函数关系是y=at﹣1(a>0,且a≠1),它的图象如图所示.给出以下命题: ①池塘中原有浮草的面积是0.5m2;
②到第7个月浮草的面积一定能超过60m2
③浮草每月增加的面积都相等;
④若浮草面积达到4m2 , 16m2 , 64m2所经过时间分别为t1 , t2 , t3 , 则t1+t2<t3 , 其中所有正确命题的序号是( )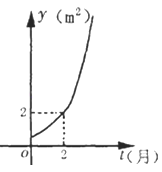
A.①②
B.①④
C.②③
D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com