
【题目】已知点![]() 到抛物线C:y2=2px
到抛物线C:y2=2px![]() 准线的距离为2.
准线的距离为2.
(Ⅰ)求C的方程及焦点F的坐标;
(Ⅱ)设点P关于原点O的对称点为点Q,过点Q作不经过点O的直线与C交于两点A,B,直线PA,PB,分别交x轴于M,N两点,求![]() 的值.
的值.
【答案】(Ⅰ)C的方程为![]() ,焦点F的坐标为(1,0);(Ⅱ)2
,焦点F的坐标为(1,0);(Ⅱ)2
【解析】
(Ⅰ)根据抛物线定义求出p,即可求C的方程及焦点F的坐标;
(Ⅱ)设点A(x1,y1),B(x2,y2),由已知得Q(1,2),由题意直线AB斜率存在且不为0,设直线AB的方程为y=k(x+1)2(k≠0),与抛物线联立可得ky2-4y+4k-8=0,利用韦达定理以及弦长公式,转化求解|MF||NF|的值.

(Ⅰ)由已知得![]() ,所以p=2.
,所以p=2.
所以抛物线C的方程为![]() ,焦点F的坐标为(1,0);
,焦点F的坐标为(1,0);
(II)设点A(x1,y1),B(x2,y2),由已知得Q(1,2),
由题意直线AB斜率存在且不为0.
设直线AB的方程为y=k(x+1)2(k≠0).
由 得
得![]() ,
,
则![]() ,
,![]() .
.
因为点A,B在抛物线C上,所以![]()
 ,
,![]() .
.
因为PF⊥x轴,
所以
 ,
,
所以|MF||NF|的值为2.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 中心在坐标原点,焦点在
中心在坐标原点,焦点在![]() 轴上,且过点
轴上,且过点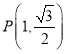 ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() 两点(
两点(![]() 两点不是左右顶点),若直线
两点不是左右顶点),若直线![]() 的斜率为
的斜率为![]() 时,弦
时,弦![]() 的中点
的中点![]() 在直线
在直线![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若在椭圆上有相异的两点![]() (
(![]() 三点不共线),
三点不共线),![]() 为坐标原点,且直线
为坐标原点,且直线![]() ,直线
,直线![]() ,直线
,直线![]() 的斜率满足
的斜率满足![]() ,求证:
,求证:![]() 是定值.
是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要制作一个如图的框架(单位:米).要求所围成的总面积为19.5(![]() ),其中
),其中![]() 是一个矩形,
是一个矩形, ![]() 是一个等腰梯形,梯形高
是一个等腰梯形,梯形高![]() ,
, ![]() ,设
,设![]() 米,
米, ![]() 米.
米.
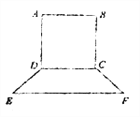
(1)求![]() 关于
关于![]() 的表达式;
的表达式;
(2)如何设计![]() ,
,![]() 的长度,才能使所用材料最少?
的长度,才能使所用材料最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图1,在Rt△ABC中,∠ACB=30°,∠ABC=90°,D为AC中点,AE![]() BD于E,延长AE交BC于F,将△ABD沿BD折起,使平面ABD
BD于E,延长AE交BC于F,将△ABD沿BD折起,使平面ABD![]() 平面BCD,如图2所示。
平面BCD,如图2所示。
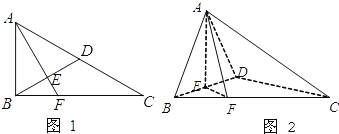
(Ⅰ)求证:AE![]() 平面BCD;
平面BCD;
(Ⅱ)求二面角A-DC-B的余弦值;
(Ⅲ)求三棱锥B-AEF与四棱锥A-FEDC的体积的比(只需写出结果,不要求过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分配![]() 名工人去
名工人去![]() 个不同的居民家里检查管道,要求
个不同的居民家里检查管道,要求![]() 名工人都分配出去,并且每名工人只去一个居民家,且每个居民家都要有人去检查,那么分配的方案共有( )
名工人都分配出去,并且每名工人只去一个居民家,且每个居民家都要有人去检查,那么分配的方案共有( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上的点到准线的最小距离为2.
上的点到准线的最小距离为2.
(1)求抛物线![]() 的方程;
的方程;
(2)若过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() ,
,![]() ,
,![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,
,![]() 分别为弦
分别为弦![]() ,
,![]() 的中点,求
的中点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD![]() 中,以D为原点建立空间直角坐标系,E为B
中,以D为原点建立空间直角坐标系,E为B![]() 的中点,F为
的中点,F为![]() 的中点,则下列向量中,能作为平面AEF的法向量的是( )
的中点,则下列向量中,能作为平面AEF的法向量的是( )
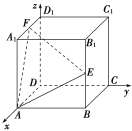
A. (1,-2,4) B. (-4,1,-2)
C. (2,-2,1) D. (1,2,-2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com