
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
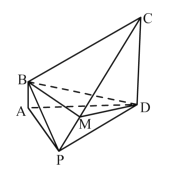
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 平面
平面![]() ,求此时直线
,求此时直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
科目:高中数学 来源: 题型:
【题目】一次循环赛中有2n+1支参赛队,其中每队与其他队均只进行一场比赛,且比赛结果中没有平局。若三支参赛队A、B、C满足:A击败B,B击败C,C击败A,则称它们形成一个“环形三元组”。求:
(1)环形三元组的最小可能数目;
(2)环形三元组的最大可能数目。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】世界那么大,我想去看看,处在具有时尚文化代表的大学生们旅游动机强烈,旅游可支配收入日益增多,可见大学生旅游是一个巨大的市场.为了解大学生每年旅游消费支出(单位:百元)的情况,相关部门随机抽取了某大学的![]() 名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
组别 |
|
|
|
|
|
频数 |
|
|
|
|
|
(Ⅰ)求所得样本的中位数(精确到百元);
(Ⅱ)根据样本数据,可近似地认为学生的旅游费用支出![]() 服从正态分布
服从正态分布![]() ,若该所大学共有学生
,若该所大学共有学生![]() 人,试估计有多少位同学旅游费用支出在
人,试估计有多少位同学旅游费用支出在![]() 元以上;
元以上;
(Ⅲ)已知样本数据中旅游费用支出在![]() 范围内的
范围内的![]() 名学生中有
名学生中有![]() 名女生,
名女生, ![]() 名男生,现想选其中
名男生,现想选其中![]() 名学生回访,记选出的男生人数为
名学生回访,记选出的男生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:若![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为![]() (t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ)写出曲线C的直角坐标方程;
(Ⅱ)若直线l与曲线C交于A,B两点,且AB的长度为2![]() ,求直线l的普通方程.
,求直线l的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 上恰有2个点到
上恰有2个点到![]() 的距离等于
的距离等于![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com