
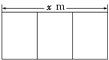
ЎҫМвДҝЎҝ ОӘБЛҫ»»Ҝ№гЦЭЛ®ПөЈ¬ДвФЪРЎЗеәУҪЁТ»ЧщЖҪГжНј(ИзНјЛщКҫ)ОӘҫШРОЗТГж»эОӘ200 m2өДИэј¶ОЫЛ®ҙҰАніШЈ¬УЙУЪөШРОПЮЦЖЈ¬іӨЎўҝн¶јІ»ДЬі¬№э16 mЈ¬Из№ыіШНвұЪҪЁФмөҘјЫОӘ400ФӘ/m2Ј¬ЦРјдБҪМхёфЗҪҪЁФмөҘјЫОӘ248ФӘ/m2Ј¬іШөЧҪЁФмөҘјЫОӘ80ФӘ/m2(іШұЪәс¶ИәцВФІ»јЖЈ¬ЗТіШОЮёЗ)Ј®
(1)РҙіцЧЬФмјЫy(ФӘ)УлxөДәҜКэ№ШПөКҪЈ¬ІўЦёіц¶ЁТеУтЈ»
(2)ЗуОЫЛ®ҙҰАніШөДіӨәНҝнёчОӘ¶аЙЩКұЈ¬ОЫЛ®ҙҰАніШөДЧЬФмјЫЧоөНЈ¬ІўЗуЧоөНФмјЫЈ®
Ўҫҙр°ёЎҝ(1) yЈҪ800xЈ«![]() Ј«16 000Ј¬
Ј«16 000Ј¬![]() ЎЬxЎЬ16.
ЎЬxЎЬ16.
(2) өұіӨОӘ16 mЈ¬ҝнОӘ12.5 mКұЈ¬ЧЬФмјЫyЧоөНЈ¬ОӘ45 000ФӘЈ®
ЎҫҪвОцЎҝ
КФМвЈЁ1Ј©ПИЗуГж»эЈ¬ФЩіЛТФ¶ФУҰјЫёсЈ¬ЗуәНөГЧЬФмјЫЈ¬ёщҫЭіӨЎўҝн¶јІ»ДЬі¬№э16 mТӘЗуИ·¶Ё¶ЁТеУтЈЁ2Ј©АыУГөјКэҝЙөГәҜКэОӘ¶ЁТеУтЙПөҘөчјхәҜКэЈ¬ФЩёщҫЭөҘөчРФЗуЧоРЎЦө
КФМвҪвОцЈәҪвЈә(1)ҫШРОЖҪГжНјөДБҪұЯіӨ·ЦұрОӘx mЈ¬![]() mЈ¬
mЈ¬
ёщҫЭМвТвЈ¬өГ
ҪвөГ![]() ЎЬxЎЬ16.
ЎЬxЎЬ16.
yЈҪ![]() ЎБ400Ј«
ЎБ400Ј«![]() ЎБ248Ј«16 000
ЎБ248Ј«16 000
ЈҪ800xЈ«![]() Ј«16 000Ј¬
Ј«16 000Ј¬![]() ЎЬxЎЬ16.
ЎЬxЎЬ16.
(2)yЎдЈҪ800Јӯ![]() Ј¬
Ј¬
өұ![]() ЎЬxЎЬ16КұЈ¬yЎдЈј0Ј¬әҜКэФЪ
ЎЬxЎЬ16КұЈ¬yЎдЈј0Ј¬әҜКэФЪ![]() ЙПОӘјхәҜКэЈ¬
ЙПОӘјхәҜКэЈ¬
ЛщТФөұіӨОӘ16 mЈ¬ҝнОӘ12.5 mКұЈ¬ЧЬФмјЫyЧоөНЈ¬ОӘ45 000ФӘЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэfЈЁxЈ©ЈҪlogaЈЁx©Ғ1Ј©ЈЁaЈҫ0Ј¬ЗТaЎЩ1Ј©Ј®
ЈЁ1Ј©ИфfЈЁxЈ©ФЪ[2Ј¬9]ЙПөДЧоҙуЦөУлЧоРЎЦөЦ®ІоОӘ3Ј¬ЗуaөДЦөЈ»
ЈЁ2Ј©ИфaЈҫ1Ј¬ЗуІ»өИКҪfЈЁ2xЈ©Јҫ0өДҪвјҜЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ОеГжМе![]() ЦРЈ¬ЛДұЯРО
ЦРЈ¬ЛДұЯРО![]() КЗБвРОЈ¬
КЗБвРОЈ¬ ![]() КЗұЯіӨОӘ2өДХэИэҪЗРОЈ¬
КЗұЯіӨОӘ2өДХэИэҪЗРОЈ¬ ![]() Ј¬
Ј¬ ![]() Ј®
Ј®
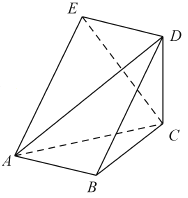
ЈЁ1Ј©ЦӨГчЈә ![]() Ј»
Ј»
ЈЁ2Ј©Иф![]() ФЪЖҪГж
ФЪЖҪГж![]() ДЪөДХэН¶У°ОӘ
ДЪөДХэН¶У°ОӘ![]() Ј¬Зуөг
Ј¬Зуөг![]() өҪЖҪГж
өҪЖҪГж![]() өДҫаАлЈ®
өДҫаАлЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЙиПтБҝ![]() Ј¬
Ј¬![]() Ј¬ФтПВБРРрКцҙнОуөДКЗ( )
Ј¬ФтПВБРРрКцҙнОуөДКЗ( )
A.Иф![]() КұЈ¬Фт
КұЈ¬Фт![]() Ул
Ул![]() өДјРҪЗОӘ¶ЫҪЗ
өДјРҪЗОӘ¶ЫҪЗ
B.![]() өДЧоРЎЦөОӘ
өДЧоРЎЦөОӘ![]()
C.Ул![]() №ІПЯөДөҘО»ПтБҝЦ»УРТ»ёцОӘ
№ІПЯөДөҘО»ПтБҝЦ»УРТ»ёцОӘ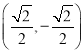
D.Иф![]() Ј¬Фт
Ј¬Фт![]() »т
»т![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝСЎРЮ4-4ЈәЧшұкПөУлІОКэ·ҪіМ
ФЪЦұҪЗЧшұкПө![]() ЦРЈ¬ЦұПЯ
ЦРЈ¬ЦұПЯ![]() ҫӯ№эөг
ҫӯ№эөг![]() Ј¬ЖдЗгРұҪЗОӘ
Ј¬ЖдЗгРұҪЗОӘ![]() Ј¬ФЪТФФӯөг
Ј¬ФЪТФФӯөг![]() ОӘј«өгЈ¬
ОӘј«өгЈ¬![]() Цб·Зёә°лЦбОӘј«ЦбөДј«ЧшұкПөЦРЈЁИЎПаН¬өДіӨ¶ИөҘО»Ј©Ј¬ЗъПЯ
Цб·Зёә°лЦбОӘј«ЦбөДј«ЧшұкПөЦРЈЁИЎПаН¬өДіӨ¶ИөҘО»Ј©Ј¬ЗъПЯ![]() өДј«Чшұк·ҪіМОӘ
өДј«Чшұк·ҪіМОӘ![]()
ЈЁўсЈ©ИфЦұПЯ![]() УлЗъПЯ
УлЗъПЯ![]() УР№«№ІөгЈ¬Зу
УР№«№ІөгЈ¬Зу![]() өДИЎЦө·¶О§Ј»
өДИЎЦө·¶О§Ј»
ЈЁўтЈ©Йи![]() ОӘЗъПЯ
ОӘЗъПЯ![]() ЙПИОТвТ»өгЈ¬Зу
ЙПИОТвТ»өгЈ¬Зу![]() өДИЎЦө·¶О§.
өДИЎЦө·¶О§.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ ЙиәҜКэf(x)ЈҪ(xЈӯ1)2Ј«bln xЈ¬ЖдЦРbОӘіЈКэЈ®
(1)өұb>![]() КұЈ¬ЕР¶ПәҜКэf(x)ФЪ¶ЁТеУтЙПөДөҘөчРФЈ»
КұЈ¬ЕР¶ПәҜКэf(x)ФЪ¶ЁТеУтЙПөДөҘөчРФЈ»
(2)ИфәҜКэf(x)УРј«ЦөөгЈ¬ЗуbөДИЎЦө·¶О§ј°f(x)өДј«ЦөөгЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘ¶Ҝөг![]() өҪ¶ЁЦұПЯ
өҪ¶ЁЦұПЯ![]() Јә
Јә![]() өДҫаАлұИөҪ¶Ёөг
өДҫаАлұИөҪ¶Ёөг![]() өДҫаАлҙу2.
өДҫаАлҙу2.
ЈЁ1Ј©Зу¶Ҝөг![]() өД№мјЈ
өД№мјЈ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁ2Ј©ФЪ![]() ЦбХэ°лЦбЙПЈ¬КЗ·сҙжФЪДіёцИ·¶ЁөДөг
ЦбХэ°лЦбЙПЈ¬КЗ·сҙжФЪДіёцИ·¶ЁөДөг![]() Ј¬№эёГөгөД¶ҜЦұПЯ
Ј¬№эёГөгөД¶ҜЦұПЯ![]() УлЗъПЯ
УлЗъПЯ![]() Ҫ»УЪ
Ҫ»УЪ![]() Ј¬
Ј¬![]() БҪөгЈ¬К№өГ
БҪөгЈ¬К№өГ![]() ОӘ¶ЁЦө.Из№ыҙжФЪЈ¬Зуіцөг
ОӘ¶ЁЦө.Из№ыҙжФЪЈ¬Зуіцөг![]() ЧшұкЈ»Из№ыІ»ҙжФЪЈ¬ЗлЛөГчАнУЙ.
ЧшұкЈ»Из№ыІ»ҙжФЪЈ¬ЗлЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪ5јюІъЖ·ЦРЈ¬УР3јюТ»өИЖ·әН2јю¶юөИЖ·Ј¬ҙУЦРИОИЎ2јюЈ¬ТФ![]() ОӘёЕВКөДКВјюКЗ(ЎЎЎЎ)
ОӘёЕВКөДКВјюКЗ(ЎЎЎЎ)
A. ЗЎУР1јюТ»өИЖ· B. ЦБЙЩУРТ»јюТ»өИЖ·
C. ЦБ¶аУРТ»јюТ»өИЖ· D. ¶јІ»КЗТ»өИЖ·
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЎчABCЦРЈ¬ҪЗAЈ¬BЈ¬CЛщ¶ФөДұЯ·ЦұрОӘaЈ¬bЈ¬cЈ¬ЗТaЈ«bЈ«cЈҪ8.
(1)ИфaЈҪ2Ј¬bЈҪ![]() Ј¬ЗуcosCөДЦөЈ»
Ј¬ЗуcosCөДЦөЈ»
(2)ИфsinAcos2![]() Ј«sinBЎӨcos2
Ј«sinBЎӨcos2![]() ЈҪ2sinCЈ¬ЗТЎчABCөДГж»эSЈҪ
ЈҪ2sinCЈ¬ЗТЎчABCөДГж»эSЈҪ![]() sinCЈ¬ЗуaәНbөДЦөЈ®
sinCЈ¬ЗуaәНbөДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com