
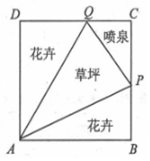
 如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a.
如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a.分析 (1)由已知利用三角函数的定义可求PB=100tanα,DQ=100tan($\frac{π}{4}$-α),利用三角形面积公式及三角函数恒等变换的应用化简可求S花卉种植面积=$\frac{5000}{\frac{\sqrt{2}}{2}sin(2α+\frac{π}{4})+\frac{1}{2}}$,其中α∈[0,$\frac{π}{4}$],利用正弦函数的性质可求最小值.
(2)设∠PAB=α,∠QAD=β,CP=x,CQ=y,则可求BP,DQ,利用两角和的正切函数公式可求tan(α+β)=$\frac{20000-100(x+y)}{100(x+y)-xy}$,由题意PB+DQ=PQ,可求:x+y=100+$\frac{xy}{200}$,即可得解tan(α+β)=1,可求α+β=$\frac{π}{4}$,即可得解.
解答 (本题满分为12分)
解:(1)∵边长为1百米的正方形ABCD中,∠PAB=a,∠PAQ=$\frac{π}{4}$,
∴PB=100tanα,DQ=100tan($\frac{π}{2}$-α-$\frac{π}{4}$)=100tan($\frac{π}{4}$-α),
∴S花卉种植面积=S△ABP+S△ADQ=$\frac{1}{2}AB•BP+\frac{1}{2}AD•DQ$=$\frac{1}{2}×$100×100tanα+$\frac{1}{2}×100×$100tan($\frac{π}{4}$-α)
=$\frac{5000}{cosα(sinα+cosα)}$=$\frac{5000}{\frac{\sqrt{2}}{2}sin(2α+\frac{π}{4})+\frac{1}{2}}$,其中α∈[0,$\frac{π}{4}$],
∴当sin(2α+$\frac{π}{4}$)=1时,即θ=$\frac{π}{4}$时,S取得最小值为5000(2-$\sqrt{2}$).…(8分)
(2)设∠PAB=α,∠QAD=β,CP=x,CQ=y,则BP=100-x,DQ=100-y,
在△ABP中,tanα=$\frac{100-x}{100}$,在△ADQ中,tanβ=$\frac{100-y}{100}$,
∴tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=$\frac{20000-100(x+y)}{100(x+y)-xy}$,
∵PB+DQ=PQ,
∴100-x+100-y=$\sqrt{{x}^{2}+{y}^{2}}$,整理可得:x+y=100+$\frac{xy}{200}$,
∴tan(α+β)=$\frac{20000-100×(100+\frac{xy}{200})}{100×(100+\frac{xy}{200})-xy}$=$\frac{10000-\frac{xy}{2}}{10000-\frac{xy}{2}}$=1,
∴α+β=$\frac{π}{4}$,
∴∠PAQ是定值,且∠PAQ=$\frac{π}{4}$.-----------(12分)
点评 本题主要考查了三角函数的定义,三角形面积公式,三角函数恒等变换的应用,正弦函数的性质,两角和的正切函数公式的综合应用,考查了转化思想和数形结合思想,属于中档题.


科目:高中数学 来源: 题型:选择题
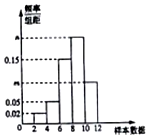 有一个容量为100的样本,其频率分布直方图如图所示,已知样本数据落在区间[10,12)内的频数比样本数据落在区间[8,10)内的频数少12,则实数m的值等于( )
有一个容量为100的样本,其频率分布直方图如图所示,已知样本数据落在区间[10,12)内的频数比样本数据落在区间[8,10)内的频数少12,则实数m的值等于( )| A. | 0.10 | B. | 0.11 | C. | 0.12 | D. | 0.13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
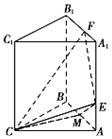 在三棱柱ABC-A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AAl,A1B1上,且AE=$\frac{1}{2}$,A1F=$\frac{3}{4}$,CE⊥EF,M为AB中点
在三棱柱ABC-A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AAl,A1B1上,且AE=$\frac{1}{2}$,A1F=$\frac{3}{4}$,CE⊥EF,M为AB中点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com