
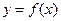 的反函数.定义:若对给定的实数
的反函数.定义:若对给定的实数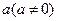 ,函数
,函数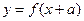 与
与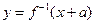 互为反函数,则称
互为反函数,则称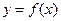 满足“
满足“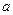 和性质”;若函数
和性质”;若函数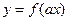 与
与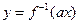 互为反函数,则称
互为反函数,则称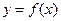 满足“
满足“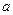 积性质”.
积性质”.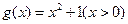 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;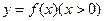 对任何
对任何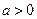 ,满足“
,满足“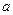 积性质”.求
积性质”.求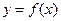 的表达式.
的表达式.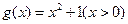 的反函数是
的反函数是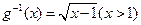 ,
,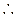
 ,
,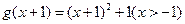 ,其反函数为
,其反函数为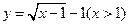
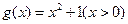 不满足“1和性质” …… 4分
不满足“1和性质” …… 4分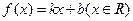 满足“2和性质”,
满足“2和性质”,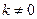 .
.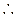
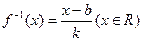 ,
,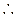
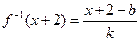 …… 6分
…… 6分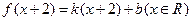 ,得反函数
,得反函数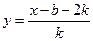 ,…… 8分
,…… 8分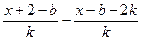 对
对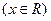 恒成立.
恒成立.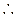
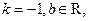 即所求一次函数
即所求一次函数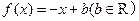 . ……10分
. ……10分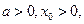 且点
且点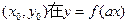 图像上,则
图像上,则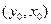 在函数
在函数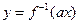 图像上,
图像上,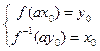 可得
可得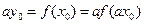 , ……12分
, ……12分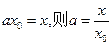 ,
,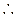
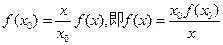 . ……14分
. ……14分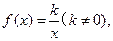 此时
此时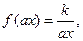 其反函数是
其反函数是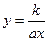 ,
,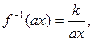 故
故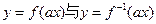 互为反函数. ……16分
互为反函数. ……16分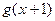 的反函数和
的反函数和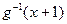 ,然后对照,如果解析式相同,就满足“1和性质”,否则,不满足;
,然后对照,如果解析式相同,就满足“1和性质”,否则,不满足;

 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源:不详 题型:解答题
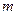 人,每人每年可创利100千元.据测算,若裁员人数不超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利1千元;若裁员人数超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利2千元.为保证公司的正常运转,留岗的员工数不得少于现有员工人数的75%.为保障被裁员工的生活,公司要付给被裁员工每人每年20千元的生活费.
人,每人每年可创利100千元.据测算,若裁员人数不超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利1千元;若裁员人数超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利2千元.为保证公司的正常运转,留岗的员工数不得少于现有员工人数的75%.为保障被裁员工的生活,公司要付给被裁员工每人每年20千元的生活费.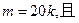 15<
15<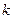 <50,为了获得最大的经济效益,该公司应裁员多少人?
<50,为了获得最大的经济效益,该公司应裁员多少人?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x |
| x2+x+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com