
(本小题满分14分)
某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划成一个矩形高科技工业园区.已知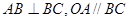 且
且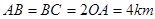 ,曲线段
,曲线段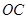 是以点
是以点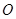 为顶点且开口向右的抛物线的一段.
为顶点且开口向右的抛物线的一段.
(I)建立适当的坐标系,求曲线段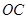 的方程;
的方程;
(II)如果要使矩形的相邻两边分别落在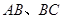 上,且一个顶点
上,且一个顶点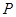 落在曲线段
落在曲线段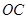 上,问如何规划才能使矩形工业园区的用地面积最大?并求这个最大值.
上,问如何规划才能使矩形工业园区的用地面积最大?并求这个最大值.

(I) 以O为原点,OA所在直线为y轴建立直角坐标系(如图),
依题可设抛物线方程为y2=2px(p>0),且C(4,2).由此可得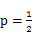 ,
,
故曲线段OC的方程为y2=x(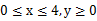 ).……………………………6分
).……………………………6分
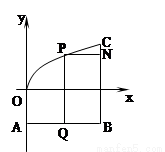 (II) 设P(t2,t)(
(II) 设P(t2,t)(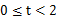 ),
),
则在矩形PQBN中,|PQ|=2+t,|PN|=4-t2.
工业园区面积S(t)=|PQ||PN|=(2+t)( 4-t2)= -t3-2t2+4t+8.
……………………………8分
导数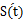 = -3t2-4t+4,
= -3t2-4t+4,
当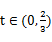 时,
时,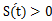 ; 当
; 当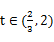 时,
时,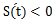 .
.
所以S(t)在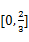 上为增函数,在
上为增函数,在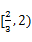 上为减函数…………10分.
上为减函数…………10分.
所以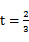 时,Smax=
时,Smax=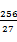 ;此时
;此时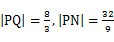 .…………13分
.…………13分
答:当矩形的长为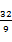 km,宽为
km,宽为 km时,园区面积最大,最大值为
km时,园区面积最大,最大值为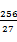 km2.-----14分
km2.-----14分
【解析】略


科目:高中数学 来源: 题型:
| 3 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)设椭圆C1的方程为![]() (a>b>0),曲线C2的方程为y=
(a>b>0),曲线C2的方程为y=![]() ,且曲线C1与C2在第一象限内只有一个公共点P。(1)试用a表示点P的坐标;(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式。
,且曲线C1与C2在第一象限内只有一个公共点P。(1)试用a表示点P的坐标;(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式。
查看答案和解析>>
科目:高中数学 来源:2011年江西省抚州市教研室高二上学期期末数学理卷(A) 题型:解答题
(本小题满分14分)
已知 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
.
(1)证明:数列 }是等比数列;
}是等比数列;
(2)设 ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式;
(3)记 ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
.
查看答案和解析>>
科目:高中数学 来源:2015届山东省威海市高一上学期期末考试数学试卷(解析版) 题型:解答题
(本小题满分14分)
某网店对一应季商品过去20天的销售价格及销售量进行了监测统计发现,第 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 天的销售量为
天的销售量为 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元.
(Ⅰ)写出销售额 关于第
关于第 天的函数关系式;
天的函数关系式;
(Ⅱ)求该商品第7天的利润;
(Ⅲ)该商品第几天的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省高三下学期第一次月考文科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行.
⑴ 求 ,
, 满足的关系式;
满足的关系式;
⑵ 若 上恒成立,求
上恒成立,求 的取值范围;
的取值范围;
⑶ 证明: (
( )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com