
【题目】某市民用水拟实行阶梯水价,每人用水量中不超过![]() 立方米的部分按4元/立方米收费,超出
立方米的部分按4元/立方米收费,超出![]() 立方米的部分按10元/立方米收费,从该市随机调查了10000位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图:
立方米的部分按10元/立方米收费,从该市随机调查了10000位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图:
(1)如果![]() 为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米,
为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米, ![]() 至少定为多少?
至少定为多少?
(2)假设同组中的每个数据用该组区间的右端点值代替,当![]() 时,估计该市居民该月的人均水费.
时,估计该市居民该月的人均水费.
 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
【题目】已知高中学生的数学成绩与物理成绩具有线性相关关系,在一次考试中某班7名学生的数学成绩与物理成绩如下表:
数学成绩 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理成绩 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
(1)求这7名学生的数学成绩的极差和物理成绩的平均数;
(2)求物理成绩![]() 对数学成绩
对数学成绩![]() 的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
下列公式与数据可供参考:
用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: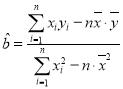 ,
,![]() ;
;
![]() ,
,![]() ,
,
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点
的焦点![]() 且斜率为1的直线与抛物线
且斜率为1的直线与抛物线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)点![]() 是抛物线
是抛物线![]() 上异于
上异于![]() 、
、![]() 的任意一点,直线
的任意一点,直线![]() 、
、![]() 与抛物线
与抛物线![]() 的准线分别交于点
的准线分别交于点![]() 、
、![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种新产品投放市场一段时间后,经过调研获得了时间![]() (天数)与销售单价
(天数)与销售单价![]() (元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图).
(元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图).
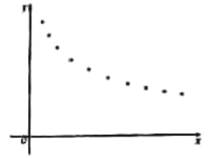
|
|
|
|
|
|
|
1.63 | 37.8 | 0.89 | 5.15 | 0.92 |
| 18.40 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适合作价格
哪一个更适合作价格![]() 关于时间
关于时间![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程.
的回归方程.
(3)若该产品的日销售量![]() (件)与时间
(件)与时间![]() 的函数关系为
的函数关系为![]() ,求该产品投放市场第几天的销售额最高?最高为多少元?
,求该产品投放市场第几天的销售额最高?最高为多少元?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为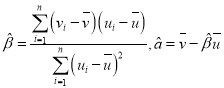 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知从![]() 地到
地到![]() 地有两条道路可以到达,走道路①准点到达的概率为
地有两条道路可以到达,走道路①准点到达的概率为![]() ,不准点到达的概率为
,不准点到达的概率为![]() ;走道路②准点到达的概率为
;走道路②准点到达的概率为![]() ,不准点到达的概率为
,不准点到达的概率为![]() .若甲乙两车走道路①,丙车由于其他原因走道路②,且三辆车是否准点到达相互之间没有影响.
.若甲乙两车走道路①,丙车由于其他原因走道路②,且三辆车是否准点到达相互之间没有影响.
(1)若三辆车中恰有一辆车没有准点到达的概率为![]() ,求走道路②准点到达的概率
,求走道路②准点到达的概率![]() ;
;
(2)在(1)的条件下,求三辆车中准点到达车辆的辆数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率是
的离心率是![]() ,A、B分别为椭圆的左顶点、上顶点,原点O到AB所在直线的距离为
,A、B分别为椭圆的左顶点、上顶点,原点O到AB所在直线的距离为![]() .
.
(I)求椭圆C的方程;
(Ⅱ)已知直线![]() 与椭圆相交于不同的两点M,N(均不是长轴的端点),
与椭圆相交于不同的两点M,N(均不是长轴的端点),![]() ,垂足为H,且
,垂足为H,且![]() ,求证:直线
,求证:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com