
| 1 |
| x-1 |
| 3 |
| m |
| 3 |
| 1 |
| lgx |
| 1 |
| x-1 |
| 1 |
| x-1 |
(x-1)•
|
| 1 |
| x-1 |
| 1 |
| 2x |
| 1 |
| 4 |
| 17 |
| 4 |
| 3 |
| m2 |
| m2-3 |
| m2 |
| 3 |
| m |
| 3 |
| 1 |
| 1 |
| lgx |
lgx•
|


科目:高中数学 来源: 题型:
| 3 |
| 2 |
| n | an |
| 1 |
| 2 |
| 7 |
| 3 |
| 1 |
| 27 |
| A、①② | B、②③ | C、③④ | D、②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2+1 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:吉林省实验中学2012届高三第六次模拟考试数学理科试题 题型:022
已知定义在[1,+∞)上的函数f(x)=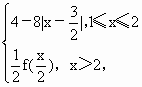 .给出下列结论:
.给出下列结论:
①函数f(x)的值域为[0,4];
②关于x的方程f(x)=(![]() )n(n∈N*)有2n+4个不相等的实数根;
)n(n∈N*)有2n+4个不相等的实数根;
③当x∈[2n-1,2n](n∈N*)时,函数f(x)的图象与x轴围成的图形面积为S,则S=2;
④存在x0∈[1,8],使得不等式x0f(x0)>6成立,
其中你认为正确的所有结论的序号为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com