
【题目】已知抛物线![]() 的焦点曲线
的焦点曲线![]() 的一个焦点,
的一个焦点, ![]() 为坐标原点,点
为坐标原点,点![]() 为抛物线
为抛物线![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 轴的平行线交抛物线的准线于
轴的平行线交抛物线的准线于![]() ,直线
,直线![]() 交抛物线于点
交抛物线于点![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)求证:直线![]() 过定点
过定点![]() ,并求出此定点的坐标.
,并求出此定点的坐标.
【答案】(I)![]() ;(II)证明见解析.
;(II)证明见解析.
【解析】试题分析:(Ⅰ)将曲线![]() 化为标准方程,可求得
化为标准方程,可求得![]() 的焦点坐标分别为
的焦点坐标分别为![]() ,可得
,可得![]() ,所以
,所以![]() ,即抛物线的方程为
,即抛物线的方程为![]() ;(Ⅱ)结合(Ⅰ),可设
;(Ⅱ)结合(Ⅰ),可设![]() ,得
,得 ,从而直线
,从而直线![]() 的方程为
的方程为![]() ,联立直线与抛物线方程得
,联立直线与抛物线方程得![]() ,解得
,解得![]() ,直线
,直线![]() 的方程为
的方程为 ,整理得
,整理得![]() 的方程为
的方程为![]() ,此时直线恒过定点
,此时直线恒过定点![]() .
.
试题解析:(Ⅰ)由曲线![]() ,化为标准方程可得
,化为标准方程可得 , 所以曲线
, 所以曲线 是焦点在
是焦点在![]() 轴上的双曲线,其中
轴上的双曲线,其中![]() ,故
,故![]() ,
, ![]() 的焦点坐标分别为
的焦点坐标分别为![]() ,因为抛物线的焦点坐标为
,因为抛物线的焦点坐标为![]() ,由题意知
,由题意知![]() ,所以
,所以![]() ,即抛物线的方程为
,即抛物线的方程为![]() .
.
(Ⅱ)由(Ⅰ)知抛物线![]() 的准线方程为
的准线方程为![]() ,设
,设![]() ,显然
,显然![]() .故
.故 ,从而直线
,从而直线![]() 的方程为
的方程为![]() ,联立直线与抛物线方程得
,联立直线与抛物线方程得![]() ,解得
,解得![]()
①当![]() ,即
,即![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,
,
②当![]() ,即
,即![]() 时,直线
时,直线![]() 的方程为
的方程为 ,整理得
,整理得![]() 的方程为
的方程为![]() ,此时直线恒过定点
,此时直线恒过定点![]() ,
, ![]() 也在直线
也在直线![]() 的方程为
的方程为![]() 上,故直线
上,故直线![]() 的方程恒过定点
的方程恒过定点![]() .
.
【题型】解答题
【结束】
21
【题目】已知函数![]() ,
, ![]()
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)若![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若数列![]() 满足
满足![]() ,
, ![]() ,记
,记![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() .
.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)证明见解析.
;(III)证明见解析.
【解析】试题分析:(Ⅰ)求出![]() ,在定义域内,分别令
,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(Ⅱ)当
的减区间;(Ⅱ)当![]() 时,因为
时,因为![]() ,所以
,所以![]() 显然不成立,先证明因此
显然不成立,先证明因此![]() 时,
时, ![]() 在
在![]() 上恒成立,再证明当
上恒成立,再证明当![]() 时不满足题意,从而可得结果;(III)先求出等差数列的前
时不满足题意,从而可得结果;(III)先求出等差数列的前![]() 项和为
项和为![]() ,结合(II)可得
,结合(II)可得![]() ,各式相加即可得结论.
,各式相加即可得结论.
试题解析:(Ⅰ)由![]() ,得
,得![]() .所以
.所以![]()
令![]() ,解得
,解得![]() 或
或![]() (舍去),所以函数
(舍去),所以函数![]() 的单调递减区间为
的单调递减区间为 ![]() .
.
(Ⅱ)由![]() 得,
得, ![]()
当![]() 时,因为
时,因为![]() ,所以
,所以![]() 显然不成立,因此
显然不成立,因此![]() .
.
令![]() ,则
,则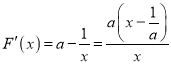 ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时, ![]() ,
, ![]() ,∴
,∴![]() ,所以
,所以![]() ,即有
,即有![]() .
.
因此![]() 时,
时, ![]() 在
在![]() 上恒成立.
上恒成立.
②当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
∴![]() ,不满足题意.
,不满足题意.
综上,不等式![]() 在
在![]() 上恒成立时,实数
上恒成立时,实数![]() 的取值范围是
的取值范围是![]() .
.
(III)证明:由![]() 知数列
知数列![]() 是
是![]() 的等差数列,所以
的等差数列,所以![]()
所以![]()
由(Ⅱ)得, ![]() 在
在![]() 上恒成立.
上恒成立.
所以![]() . 将以上各式左右两边分别相加,得
. 将以上各式左右两边分别相加,得
![]() .因为
.因为![]()
所以![]()
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是矩形,面
是矩形,面![]() 底面
底面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() 在
在![]() 上,且
上,且![]() 面
面![]() .
.

(1)求证: ![]() 是
是![]() 的中点;
的中点;
(2)在![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 为直角?若存在,求出
为直角?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人各进行3次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率为
,乙每次击中目标的概率为![]() 。
。
(1)记甲击中目标的次数为![]() ,求
,求![]() 的概率分布及数学期望;
的概率分布及数学期望;
(2)求乙至多击目标2次的概率;
(3)求甲恰好比乙多击中目标2次的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校高三年级800名学生中随机抽取50名测量身高,据测量被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…第八组[190,195],图是按上述分组方法得到的条形图.

(1)根据已知条件填写将表格填写完整;
组别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
样本 | 2 | 4 | 10 | 10 | 15 | 4 |
(2)估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数;
(3)在样本中,若第二组有1人为男生,其余为女生,第七组有1人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月22日.在平昌冬奥会短道速滑男子500米比赛中.中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造中国男子冰上竞速项目在冬奥会金牌零的突破.某高校为调查该校学生在冬奥会期间累计观看冬奥会的时间情况.收集了200位男生、100位女生累计观看冬奥会时间的样本数据(单位:小时).又在100位女生中随机抽取20个人.已知这20位女生的数据茎叶图如图所示.
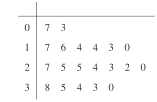
(1)将这20位女生的时间数据分成8组,分组区间分别为![]() ,在答题卡上完成频率分布直方图;
,在答题卡上完成频率分布直方图;
(2)以(1)中的频率作为概率,求1名女生观看冬奥会时间不少于30小时的概率;
(3)以(1)中的频率估计100位女生中累计观看时间小于20个小时的人数.已知200位男生中累计观看时间小于20小时的男生有50人请完成答题卡中的列联表,并判断是否有99 %的把握认为“该校学生观看冬奥会累计时间与性别有关”.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
附:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净。假设1千克该蔬菜用清水![]() 千克清洗后,蔬菜上残留的农药为
千克清洗后,蔬菜上残留的农药为![]() 微克,通过样本数据得到
微克,通过样本数据得到![]() 关于
关于![]() 的散点图。由数据分析可用函数
的散点图。由数据分析可用函数![]() 拟合
拟合![]() 与
与![]() 的关系.
的关系.

(1)求![]() 与
与![]() 的回归方程
的回归方程![]() (
(![]() 精确到0.1);
精确到0.1);
(2)已知对于残留在蔬菜上的农药,当它的残留量不超过20微克时对人体无害。为了放心食用该蔬菜,请估计至少需要用多少克的清水清洗1千克蔬菜?(答案精确到0.1)
附:①参考数据:![]() ,
,![]() ,
,![]() (其中
(其中![]() ),
),![]() 。
。
②参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2011年至2017年农村居民家庭人均纯收入(单位:千元)的数据如下表:

(I)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(II)利用(I)中所求的线性回归方程,分析该地区2011年至2017年农村居民家庭人均纯收入的变化情况,并预测该地区2018年农村居民家庭人均纯收入.
参考公式: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为“中学数学联赛”选拔人才,分初赛和复赛两个阶段进行,规定:分数不小于本次考试成绩中位数的具有复赛资格,某校有900名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图.
内,其频率分布直方图如图.

(1)求获得复赛资格应划定的最低分数线;
(2)从初赛得分在区间![]() 的参赛者中,利用分层抽样的方法随机抽取7人参加学校座谈交流,那么从得分在区间
的参赛者中,利用分层抽样的方法随机抽取7人参加学校座谈交流,那么从得分在区间![]() 与
与![]() 各抽取多少人?
各抽取多少人?
(3)从(2)抽取的7人中,选出4人参加全市座谈交流,设![]() 表示得分在
表示得分在![]() 中参加全市座谈交流的人数,学校打算给这4人一定的物质奖励,若该生分数在
中参加全市座谈交流的人数,学校打算给这4人一定的物质奖励,若该生分数在![]() 给予500元奖励,若该生分数在
给予500元奖励,若该生分数在![]() 给予800元奖励,用Y表示学校发的奖金数额,求Y的分布列和数学期望。
给予800元奖励,用Y表示学校发的奖金数额,求Y的分布列和数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com