
【题目】已知函数![]() .
.
(1)过原点![]() 作函数
作函数![]() 图象的切线,求切点的横坐标;
图象的切线,求切点的横坐标;
(2)对![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(1)设切点坐标,利用导数几何意义以及切点在切线上,也在曲线上列方程组,解得切点的横坐标;(2)不等式恒成立问题往往转化为对应函数最值问题: ![]() 对
对![]() ,
, ![]() 恒成立等价于
恒成立等价于![]() 的最小值不小于零,根据导函数符号变化规律,分类讨论函数单调性,进而得函数最值,验证是否满足条件,确定实数
的最小值不小于零,根据导函数符号变化规律,分类讨论函数单调性,进而得函数最值,验证是否满足条件,确定实数![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)设切点为![]() ,直线的切线方程为
,直线的切线方程为![]()
, ![]() ,
,
即直线的切线方程为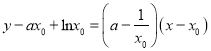
又切线过原点![]() ,所以
,所以![]() ,
,
由![]() ,解得
,解得![]() ,所以切点的横坐标为
,所以切点的横坐标为![]() .
.
(Ⅱ)方法一:∵不等式![]() 对
对![]() ,
, ![]() 恒成立,
恒成立,
∴![]() 对
对![]() ,
, ![]() 恒成立.
恒成立.
设![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
①当![]() 时,
时, ![]() ,
, ![]() 在
在![]() ,
, ![]() 上单调递减,
上单调递减,
即![]() ,
, ![]() 不符合题意.
不符合题意.
②当![]() 时,
时, ![]() .设
.设![]() ,
,
在![]() ,
, ![]() 上单调递增,即
上单调递增,即![]() .
.
(ⅰ)当![]() 时,由
时,由![]() ,得
,得![]() ,
, ![]() 在
在![]() ,
, ![]() 上单调递增,即
上单调递增,即![]() ,
, ![]() 符合题意;
符合题意;
(ii)当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 使得
使得![]() ,
,
则![]() 在
在![]() ,
, ![]() 上单调递减,在
上单调递减,在![]() ,
, ![]() 上单调递增,
上单调递增,
![]() ,则
,则![]() 不合题意.
不合题意.
综上所述, ![]() .
.
(Ⅱ)方法二:∵不等式![]() 对
对![]() ,
, ![]() 恒成立,
恒成立,
∴![]() 对
对![]() ,
, ![]() 恒成立.
恒成立.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
![]() 不恒成立;同理
不恒成立;同理![]() 取其他值不恒成立.
取其他值不恒成立.
当![]() 时,
时, ![]() 恒成立;
恒成立;
当![]() 时,
时, ![]() ,证明
,证明![]() 恒成立.
恒成立.
设![]()
![]() ,
, ![]() ,
,
![]() .∴
.∴![]() 在
在![]() ,
, ![]() 为减函数.
为减函数.
![]() ,∴
,∴![]() .
.
(Ⅱ)方法三:∵不等式![]() 对
对![]() ,
,![]() 恒成立,
恒成立,
∴等价于![]() 对
对![]() ,
, ![]() 恒成立.
恒成立.
设![]() ,当
,当![]() 时,
时, ![]() ;∴
;∴![]() ,
,
函数![]() 过点(0,0)和(1,0),函数
过点(0,0)和(1,0),函数![]() 过点(1.0),
过点(1.0),![]() 在
在![]() 恒成立,
恒成立,
一定存在一条过点(1,0)的直线和函数![]() 、
、![]() 都相切或,一定存在一条过点(1,0)的直线
都相切或,一定存在一条过点(1,0)的直线![]() 相切和函数
相切和函数![]() 相交,但交点横坐标小于1,
相交,但交点横坐标小于1,
当都相切时![]() .
.
![]() 不大于等于0.
不大于等于0.
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() (
(![]() ),圆
),圆![]() (
(![]() ),若圆
),若圆![]() 的一条切线
的一条切线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)当![]() ,
, ![]() 时,若点
时,若点![]() 都在坐标轴的正半轴上,求椭圆
都在坐标轴的正半轴上,求椭圆![]() 的方程;
的方程;
(2)若以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,探究
,探究![]() 之间的等量关系,并说明理由.
之间的等量关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时, ![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴左侧的图象,如图所示,并根据图象:
轴左侧的图象,如图所示,并根据图象:

(1)直接写出函数![]() ,
, ![]() 的增区间;
的增区间;
(2)写出函数![]() ,
, ![]() 的解析式;
的解析式;
(3)若函数![]() ,
, ![]() ,求函数
,求函数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-a|.
(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃.下面叙述不正确的是 ( )
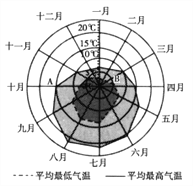
A. 各月的平均最低气温都在0℃以上
B. 七月的平均温差比一月的平均温差大
C. 三月和十一月的平均最高气温基本相同
D. 平均最高气温高于20℃的月份有5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,已知椭圆![]() 的上顶点为
的上顶点为![]() ,左、右顶点为
,左、右顶点为![]() ,右焦点为
,右焦点为![]() ,
, ![]() ,且
,且![]() 的周长为14.
的周长为14.
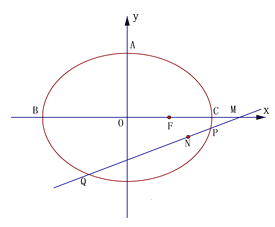
(I)求椭圆的离心率;
(II)过点![]() 的直线
的直线![]() 与椭圆相交于不同两点
与椭圆相交于不同两点![]() ,点N在线段
,点N在线段![]() 上.设
上.设![]() ,试判断点
,试判断点![]() 是否在一条定直线上,并求实数λ的取值范围.
是否在一条定直线上,并求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com