
【题目】写出下列命题的否定,并判断所得命题的真假:
(1)二次函数![]() 的图像的顶点坐标是
的图像的顶点坐标是![]() ;
;
(2)正数的立方根都是正数;
(3)存在一个最大的内角小于60°的三角形;
(4)对任意实数t,点![]() 都在一次函数
都在一次函数![]() 的图像上.
的图像上.
【答案】(1)二次函数![]() 的顶点坐标不是
的顶点坐标不是![]() ,假命题;
,假命题;
(2)正数的立方根不都是正数,假命题;
(3)任意三角形的最大内角不小于60°,真命题;
(4)至少有一个实数t,点![]() 不在一次函数
不在一次函数![]() 的图像上,假命题.
的图像上,假命题.
【解析】
根据命题的否定的定义,题设不变,结论否定,写出其命题的否定;当命题含有量词则需将量词改变,结论否定.
解:(1)![]() 二次函数
二次函数![]() 的图像的顶点坐标是
的图像的顶点坐标是![]() ;
;
所以其否定为:二次函数![]() 的图像的顶点坐标不是
的图像的顶点坐标不是![]() ;
;
因为原命题是真命题,故其否定为假命题;
(2)![]() 命题“正数的立方根都是正数”是全称命题;
命题“正数的立方根都是正数”是全称命题;
所以其否定为:存在正数的立方根不是正数,
由原命题是真命题,故其否定为假命题;
(3)![]() 命题“存在一个最大的内角小于60°的三角形”是特称命题,
命题“存在一个最大的内角小于60°的三角形”是特称命题,
所以其否定为:任意三角形的最大内角不小于60°,因为原命题是假命题,故其否定是真命题;
(4)![]() 命题“对任意实数t,点
命题“对任意实数t,点![]() 都在一次函数
都在一次函数![]() 的图像上.” 是全称命题.
的图像上.” 是全称命题.
所以其否定为:至少有一个实数t,点![]() 不在一次函数
不在一次函数![]() 的图像上,
的图像上,
显然原命题为真命题,故其否定为假命题.


科目:高中数学 来源: 题型:
【题目】将一枚质地均匀的硬币连掷![]() 次,设事件
次,设事件![]() “恰好两次正面朝上”,
“恰好两次正面朝上”,
(1)直接计算事件![]() 的概率;
的概率;
(2)利用计算器或计算机模拟试验80次,计算事件![]() 发生的频率.
发生的频率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏,从中部选择河北. 湖北,从西部选择宁夏,从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记.由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验.在某普查小区,共有 50 家企事业单位,150 家个体经营户,普查情况如下表所示:
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 50 | |
个体经营户 | 50 | 150 | |
合计 |
(1)写出选择 5 个国家综合试点地区采用的抽样方法;
(2)补全上述列联表(在答题卡填写),并根据列联表判断是否有![]() 的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3)根据该试点普查小区的情况,为保障第四次经济普查的顺利进行,请你从统计的角度提出一条建议.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华中师大附中中科教处为了研究高一学生对物理和数学的学习是否与性别有关,从高一年级抽取60,名同学(男同学30名,女同学30名),给所有同学物理题和数学题各一题,让每位同学自由选择一道题进行解答.选题情况如下表:(单位:人)

(1)在犯错误的概率不超过1%是条件下,能否判断高一学生对物理和数学的学习与性别有关?
(2)经过多次测试后发现,甲每次解答一道物理题所用的时间5—8分钟,乙每次解答一道物理题所用的时间为6—8分钟,现甲、乙解同一道物理题,求甲比乙先解答完的概率;
(3)现从选择做物理题的8名女生中任意选取两人,对题目的解答情况进行全程研究,记甲、乙两女生被抽到的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某电子元件进行寿命追踪调查,情况如下:
寿命分组/h | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
个数 | 20 | 30 | 80 | 40 | 30 |
(1)求下表中的x,y;
寿命分组/h | 频数 | 频率 |
100~200 | 20 | 0.10 |
200~300 | 30 | x |
300~400 | 80 | 0.40 |
400~500 | 40 | 0.20 |
500~600 | 30 | y |
合计 | 200 | 1 |
(2)从频率分布直方图估计电子元件寿命的第80百分位数是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是R上的偶函数,对于
是R上的偶函数,对于![]() 都有
都有![]() 成立,且
成立,且![]() ,当
,当![]() ,且
,且![]() 时,都有
时,都有![]() .则给出下列命题:
.则给出下列命题:
①![]() ;
;
②函数![]() 图象的一条对称轴为
图象的一条对称轴为![]() ;
;
③函数![]() 在[﹣9,﹣6]上为减函数;④方程
在[﹣9,﹣6]上为减函数;④方程![]() 在[﹣9,9]上有4个根;
在[﹣9,9]上有4个根;
其中正确的命题序号是___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
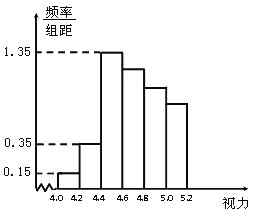

(1)若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50的学生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:

![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】互联网正在改变着人们的生活方式,在日常消费中手机支付正逐渐取代现金支付成为人们首选的支付方式. 某学生在暑期社会活动中针对人们生活中的支付方式进行了调查研究. 采用调查问卷的方式对100名18岁以上的成年人进行了研究,发现共有60人以手机支付作为自己的首选支付方式,在这60人中,45岁以下的占![]() ,在仍以现金作为首选支付方式的人中,45岁及以上的有30人.
,在仍以现金作为首选支付方式的人中,45岁及以上的有30人.
(1)从以现金作为首选支付方式的40人中,任意选取3人,求这3人至少有1人的年龄低于45岁的概率;
(2)某商家为了鼓励人们使用手机支付,做出以下促销活动:凡是用手机支付的消费者,商品一律打八折. 已知某商品原价50元,以上述调查的支付方式的频率作为消费者购买该商品的支付方式的概率,设销售每件商品的消费者的支付方式都是相互独立的,求销售10件该商品的销售额的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com