已知函数y=f(x)满足f(3x)=3f(x),当1<x<3时,f(x)=1-|x-2|,那么x∈[1,3n],n∈N*时,函数y=f(x)的图象与x轴所围成的图形面积为________.
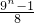
分析:由已知中当1<x<3时,f(x)=1-|x-2|,函数y=f(x)满足f(3x)=3f(x),我们可以分别求出x∈[3
n-1,3
n]时,函数y=f(x)的图象与x轴所围成的图形面积S
n-1,代入等比数列前n项和公式,即可得到答案.
解答:∵函数y=f(x)满足f(3x)=3f(x),
又∵当x∈[1,3]时,函数y=f(x)的图象与x轴所围成的图形面积S
1=
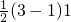
=1,
∴当x∈[3
1,3
2]时,函数y=f(x)的图象与x轴所围成的图形面积S
2=
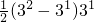
=9,
当x∈[3
2,3
3]时,函数y=f(x)的图象与x轴所围成的图形面积S
3=
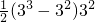
=81,
…
当x∈[3
n-1,3
n]时,函数y=f(x)的图象与x轴所围成的图形面积S
n-1=
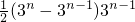
=3
2n-2此时函数y=f(x)的图象与x轴所围成的图形面积S=S
1+S
2+S
3+…+S
n-1=
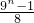
故答案为:
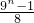
点评:本题考查的知识点是等比数列的前n项和,其中根据已知条件,确定出当x∈[3
n-1,3
n]时,函数y=f(x)的图象与x轴所围成的图形面积,成等比数列,并求出其通项公式,是解答本题的关键.

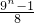
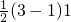 =1,
=1,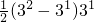 =9,
=9,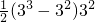 =81,
=81,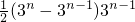 =32n-2
=32n-2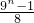
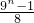


 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为