
(Ⅰ)1证明两角和的余弦公式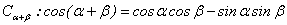 ;
;
2由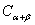 推导两角和的正弦公式
推导两角和的正弦公式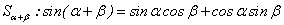 .
.
(Ⅱ)已知△ABC的面积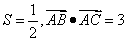 ,且
,且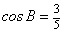 ,求cosC.
,求cosC.

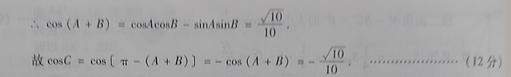
本小题主要考察两角和的正、余弦公式、诱导公式、同角三角函数间的关系等基础知识及运算能力。
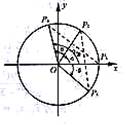 解:(1)①如图,在执教坐标系xOy内做单位圆O,并作出角α、β与-β,使角α的始边为Ox,交⊙O于点P1,终边交⊙O于P2;角β的始边为OP2,终边交⊙O于P3;角-β的始边为OP1,终边交⊙O于P4.
解:(1)①如图,在执教坐标系xOy内做单位圆O,并作出角α、β与-β,使角α的始边为Ox,交⊙O于点P1,终边交⊙O于P2;角β的始边为OP2,终边交⊙O于P3;角-β的始边为OP1,终边交⊙O于P4.
则P1(1,0),P2(cosα,sinα)
P3(cos(α+β),sin(α+β)),P4(cos(-β),sin(-β))
由P1P3=P2P4及两点间的距离公式,得
[cos(α+β)-1]2+sin2(α+β)=[cos(-β)-cosα]2+[sin(-β)-sinα]2
展开并整理得: cos(α+β)= (cosαcosβ-sinαsinβ)
∴cos(α+β)=cosαcosβ-sinαsinβ.……………………4分
②由①易得cos(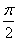 -α)=sinα,sin(
-α)=sinα,sin(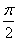 -α)=cosα
-α)=cosα
sin(α+β)=cos[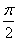 -(α+β)]=cos[(
-(α+β)]=cos[(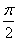 -α)+(-β)]
-α)+(-β)]
=cos(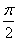 -α)cos(-β)-sin(
-α)cos(-β)-sin(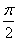 -α)sin(-β)
-α)sin(-β)
=sinαcosβ+cosαsinβ……………………………………6分
(2)由题意,设△ABC的角B、C的对边分别为b、c
则S=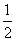 bcsinA=
bcsinA=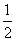
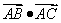 =bccosA=3>0
=bccosA=3>0
∴A∈(0,
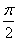 ),cosA=3sinA
),cosA=3sinA
又sin2A+cos2A=1,∴sinA= ,cosA=
,cosA=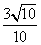
由题意,cosB=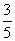 ,得sinB=
,得sinB=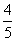
∴cos(A+B)=cosAcosB-sinAsinB=
故cosC=cos[π-(A+B)]=-cos(A+B)=- …………………………12分
…………………………12分


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com