
【题目】 设函数![]() ,其中
,其中![]() .
.
(Ⅰ)若![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(Ⅱ)若![]() ,
,
(i)证明![]() 恰有两个零点
恰有两个零点
(ii)设![]() 为
为![]() 的极值点,
的极值点,![]() 为
为![]() 的零点,且
的零点,且![]() ,证明
,证明![]() .
.
【答案】(I)![]() 在
在![]() 内单调递增.;
内单调递增.;
(II)(i)见解析;(ii)见解析.
【解析】
(I);首先写出函数的定义域,对函数求导,判断导数在对应区间上的符号,从而得到结果;
(II)(i)对函数求导,确定函数的单调性,求得极值的符号,从而确定出函数的零点个数,得到结果;
(ii)首先根据题意,列出方程组,借助于中介函数,证得结果.
(I)解:由已知,![]() 的定义域为
的定义域为![]() ,
,
且![]() ,
,
因此当![]() 时,
时,![]() ,从而
,从而![]() ,
,
所以![]() 在
在![]() 内单调递增.
内单调递增.
(II)证明:(i)由(I)知,![]() ,
,
令![]() ,由
,由![]() ,可知
,可知![]() 在
在![]() 内单调递减,
内单调递减,
又![]() ,且
,且![]() ,
,
故![]() 在
在![]() 内有唯一解,
内有唯一解,
从而![]() 在
在![]() 内有唯一解,不妨设为
内有唯一解,不妨设为![]() ,
,
则![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 内单调递增;
内单调递增;
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 内单调递减,
内单调递减,
因此![]() 是
是![]() 的唯一极值点.
的唯一极值点.
令![]() ,则当
,则当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 内单调递减,
内单调递减,
从而当![]() 时,
时,![]() ,所以
,所以![]() ,
,
从而![]() ,
,
又因为![]() ,所以
,所以![]() 在
在![]() 内有唯一零点,
内有唯一零点,
又![]() 在
在![]() 内有唯一零点1,从而,
内有唯一零点1,从而,![]() 在
在![]() 内恰有两个零点.
内恰有两个零点.
(ii)由题意,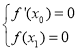 ,即
,即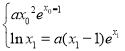 ,
,
从而![]() ,即
,即![]() ,
,
以内当![]() 时,
时,![]() ,又
,又![]() ,故
,故![]() ,
,
两边取对数,得![]() ,
,
于是![]() ,整理得
,整理得![]() ,
,


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某校计划面向高一年级![]() 名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了
名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了![]() 名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有
名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有![]() 人.在这
人.在这![]() 名学生中选择社会科学类的男生、女生均为
名学生中选择社会科学类的男生、女生均为![]() 人.
人.
(Ⅰ)分别计算抽取的样本中男生及女生选择社会科学类的频率,并以统计的频率作为概率,估计实际选课中选择社会科学类学生数;
(Ⅱ)根据抽取的![]() 名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过
名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过![]() 的前提下认为科类的选择与性别有关?
的前提下认为科类的选择与性别有关?
选择自然科学类 | 选择社会科学类 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: 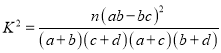 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)得到函数
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)得到函数![]() 的图象,已知函数
的图象,已知函数![]()
 ,则当函数
,则当函数![]() 有4个零点时
有4个零点时![]() 的取值集合为( )
的取值集合为( )
A. ![]()
![]() B.
B. ![]()
![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个顶点A(-1,0),B(1,0),C(3,2),其外接圆为⊙H.
(1)若直线l过点C,且被⊙H截得的弦长为2,求直线l的方程;
(2)对于线段BH上的任意一点P,若在以C为圆心的圆上都存在不同的两点M,N,使得点M是线段PN的中点,求⊙C的半径r的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为招聘新员工设计了一个面试方案:应聘者从![]() 道备选题中一次性随机抽取
道备选题中一次性随机抽取![]() 道题,按照题目要求独立完成规定:至少正确完成其中
道题,按照题目要求独立完成规定:至少正确完成其中![]() 道题的便可通过.已知
道题的便可通过.已知![]() 道备选题中应聘者甲有
道备选题中应聘者甲有![]() 道题能正确完成,
道题能正确完成,![]() 道题不能完成;应聘者乙每题正确完成的概率都是
道题不能完成;应聘者乙每题正确完成的概率都是![]() ,且每题正确完成与否互不影响
,且每题正确完成与否互不影响
(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体ABCD﹣A1B1C1D1为正方体,则下面结论正确的是( )

A.A1B∥B1C
B.平面CB1D1⊥平面A1B1C1D1
C.平面CB1D1∥平面A1BD
D.异面直线AD与CB1所成的角为30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中错误的是( )
A.样本频率分布直方图中的小矩形的面积就是对应组的频率
B.回归直线过样本点的中心![]()
C.若样本![]() 的平均数是2,方差是2,则数据
的平均数是2,方差是2,则数据![]() 的平均数是4,方差是4
的平均数是4,方差是4
D.抛掷一颗质地均匀的骰子,事件“向上点数不大于3”和事件“向上点数不小于4”是对立事件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高三理科班共有![]() 名同学参加某次考试,从中随机挑出
名同学参加某次考试,从中随机挑出![]() 名同学,他们的数学成绩
名同学,他们的数学成绩![]() 与物理成绩
与物理成绩![]() 如下表:
如下表:
数学成绩 |
|
|
|
|
|
物理成绩 |
|
|
|
|
|
(1)数据表明![]() 与
与![]() 之间有较强的线性关系,求
之间有较强的线性关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)本次考试中,规定数学成绩达到![]() 分为优秀,物理成绩达到
分为优秀,物理成绩达到![]() 分为优秀.若该班数学优秀率与物理优秀率分别为
分为优秀.若该班数学优秀率与物理优秀率分别为![]() 和
和![]() ,且除去抽走的
,且除去抽走的![]() 名同学外,剩下的同学中数学优秀但物理不优秀的同学共有
名同学外,剩下的同学中数学优秀但物理不优秀的同学共有![]() 人,请写出
人,请写出![]() 列联表,判断能否在犯错误的概率不超过
列联表,判断能否在犯错误的概率不超过![]() 的前提下认为数学优秀与物理优秀有关?
的前提下认为数学优秀与物理优秀有关?
参考数据: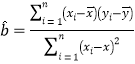 ,
,![]() ;
;![]() ,
,![]() ;
;![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com