
【题目】已知函数![]() .
.
(1)求函数![]() 的单调增区间;
的单调增区间;
(2)若存在![]() ,使得
,使得![]() (
(![]() 是自然对数的底数),求
是自然对数的底数),求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)先求原函数的导数得:f'(x)= ![]() ,再对a进行讨论,得到f'(x)>0,从而函数f(x)在(0,+∞)上单调递增.
,再对a进行讨论,得到f'(x)>0,从而函数f(x)在(0,+∞)上单调递增.
(2)f(x)的最大值减去f(x)的最小值大于或等于e﹣1,由单调性知,f(x)的最大值是f(1)或f(﹣1),最小值f(0)=1,由f(1)﹣f(﹣1)的单调性,判断f(1)与f(﹣1)的大小关系,再由f(x)的最大值减去最小值f(0)大于或等于e﹣1求出a的取值范围.
试题解析:
(1)由于![]() ,
,
1° 当![]() 单调递增,
单调递增, ![]() ,所以
,所以![]() 单调递增,
单调递增,
故![]() 单调递增,
单调递增,
∴![]() ,即
,即![]() ,所以
,所以![]() ,
,
故函数![]() 在
在![]() 上单调递增;
上单调递增;
2° 当![]() 单调递增,
单调递增, ![]() ,所以
,所以![]() 单调递增,故
单调递增,故![]() 单调递增,
单调递增,
∴![]() ,即
,即![]() ,所以
,所以![]() ,
,
故函数![]() 在
在![]() 上单调递增;综上,函数
上单调递增;综上,函数![]() 的单调增区间为
的单调增区间为![]() .
.
(2)因为存在![]() ,使得
,使得![]() ,
,
所以当![]() 时,
时, ![]() ,
,
由(1)知, ![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
所以当![]() 时
时![]() ,
,
而![]() ,
,
记![]() ,因为
,因为![]() (当
(当![]() 时取等号),
时取等号),
所以![]() 在
在![]() 上单调递增,而
上单调递增,而![]() .
.
1° 当![]() 时,
时, ![]() , ∴
, ∴![]() , ∴当
, ∴当![]() 时,
时, ![]() ,
,
即![]() ,易知:
,易知: ![]() ,在
,在![]() 上递增, ∴
上递增, ∴![]() .
.
2° 当![]() 时,
时, ![]() , ∴
, ∴![]() ,
,
易知![]() 在
在![]() 上递减, ∴
上递减, ∴![]() ,综上:
,综上: ![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)═log2( ![]() +a).
+a).
(1)若f(1)<2,求实数a的取值范围;
(2)设函数g(x)=f(x)﹣log2[(a﹣4)x+2a﹣5],讨论函数g(x)的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图象关于y轴对称,并且是[0,+∞)上的减函数,若f(lgx)>f(1),则实数x的取值范围是( )
A.![]()
B.![]()
C.![]()
D.(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了了解某地区电视观众对某体育节目的收视情况,随机抽取了100名观众进行调查,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成下面2×2列联表,并据此资料你是否认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(2)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为X,若每次抽取的结果是相互独立的,求X的分布列,期望E(X)和方差D(X)
P( K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() ,椭圆
,椭圆![]() ,
, ![]() 为椭圆
为椭圆![]() 的右顶点,过原点且异于
的右顶点,过原点且异于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于
交于![]() 两点,
两点, ![]() 在
在![]() 轴的上方,直线
轴的上方,直线![]() 与圆
与圆![]() 的另一交点为
的另一交点为![]() ,直线
,直线![]() 与圆
与圆![]() 的另一交点为
的另一交点为![]() ,
,
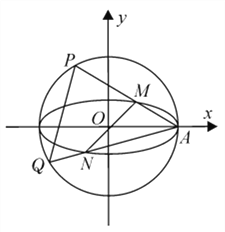
(1)若![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)设![]() 与
与![]() 的面积分别为
的面积分别为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不过第二象限的直线l:ax﹣y﹣4=0与圆x2+(y﹣1)2=5相切.
(1)求直线l的方程;
(2)若直线l1过点(3,﹣1)且与直线l平行,直线l2与直线l1关于直线y=1对称,求直线l2的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车公司为了考查某4S店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店维修或保养后可以对该店进行打分,最高分为10分.上个月公司对该4S店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:
第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到频率分布直方图如图所示.
(I)求所打分值在[6,10]的客户的人数:
(II)该公司在第二、三组客户中按分层抽样的方法抽取6名客户进行深入调查,之后将从这6人中随机抽取2人进行物质奖励,求得到奖励的人来自不同组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com