
【题目】函数f(x)=a ![]() (0<a<1)的单调递增区间是( )
(0<a<1)的单调递增区间是( )
A.(﹣∞, ![]() )
)
B.( ![]() ,+∞)
,+∞)
C.(﹣∞,﹣ ![]() )
)
D.(﹣ ![]() ,+∞)
,+∞)
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2![]() , AD=2,求四边形绕AD旋转一周所围成几何体的表面积及体积.
, AD=2,求四边形绕AD旋转一周所围成几何体的表面积及体积.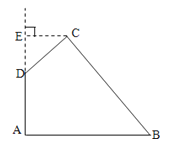
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,过椭圆
中,过椭圆![]() :
: ![]() (
(![]() )焦点的直线
)焦点的直线![]() 交
交![]() 于
于![]() 两点,
两点, ![]() 为
为![]() 的中点,且
的中点,且![]() 的斜率为9.
的斜率为9.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)![]() 是
是![]() 的左、右顶点,
的左、右顶点, ![]() 是
是![]() 上的两点,若
上的两点,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=π/2,AB=BC=2AD=4,E,F分别是AB,CD上的点,EF∥BC,AE=x,G是BC的中点,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF.
(1)当x=2时,①求证:BD⊥EG;②求二面角D﹣BF﹣C的余弦值;
(2)三棱锥D﹣FBC的体积是否可能等于几何体ABE﹣FDC体积的一半?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且a≠1,函数f(x)=loga(x+1),![]() , 记F(x)=2f(x)+g(x)
, 记F(x)=2f(x)+g(x)
(1)求函数F(x)的定义域D及其零点;
(2)若关于x的方程F(x)﹣m=0在区间[0,1)内有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A={x|2x2+ax+2=0},B={x|x2+3x﹣b=0},且A∩B={2}.
(1)求a,b的值;
(2)设全集U=AUB,求(UA)U(UB).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+4ax+2a+6.
(1)若函数f(x)=log2 f(x)的最小值为2,求a的值;
(2)若对任意x∈R,都有f(x)≥0成立,求函数g(a)=2﹣a|a+3|的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】非空集合A中的元素个数用(A)表示,定义(A﹣B)= ![]() ,若A={﹣1,0},B={x||x2﹣2x﹣3|=a},且(A﹣B)≤1,则a的所有可能值为( )
,若A={﹣1,0},B={x||x2﹣2x﹣3|=a},且(A﹣B)≤1,则a的所有可能值为( )
A.{a|a≥4}
B.{a|a>4或a=0}
C.{a|0≤a≤4}
D.{a|a≥4或a=0}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com