
(本小题共12分) 给定函数 和
和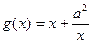
(I)求证: 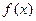 总有两个极值点;
总有两个极值点;
(II) 若
若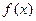 和
和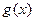 有相同的极值点,求
有相同的极值点,求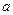 的值.
的值.
证明: (I)因为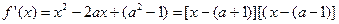 ,
,
令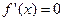 ,则
,则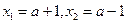 ,---------------------2分
,---------------------2分
则当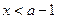 时,
时, 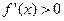 ,当
,当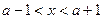 ,
, 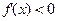
所以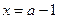 为
为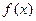 的一个极大值点, ------------4分
的一个极大值点, ------------4分
同理可证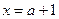 为
为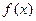 的一个极小值点.----- ----------5分
的一个极小值点.----- ----------5分
另解:(I)因为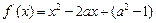 是一个二次函数,
是一个二次函数,
且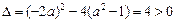 ,-------------------------------------2分
,-------------------------------------2分
所以导函数有两个不同的零点, 又因为导函数是一个二次函数,
又因为导函数是一个二次函数,
所以函数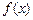 有两个不同的极值点.-------- ----------5分
有两个不同的极值点.-------- ----------5分
(II) 因为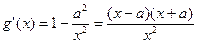 ,
,
令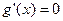 ,则
,则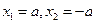 ---------------6分
---------------6分
因为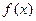 和
和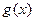 有相同的极值点, 且
有相同的极值点, 且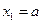 和
和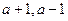 不可能相等,
不可能相等,
所以当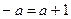 时,
时,  , 当
, 当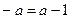 时,
时, 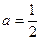 ,
,
经检验,  和
和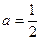 时,
时, 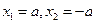 都是
都是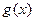 的极值点
的极值点
解析


科目:高中数学 来源: 题型:
. (本小题共12分)已知椭圆E:![]() 的焦点坐
的焦点坐![]() 标为
标为![]() (
(![]() ),点M(
),点M(![]() ,
,![]() )在椭圆E上
)在椭圆E上![]() (1)求椭圆E的方程;(2)O为坐标原点,⊙
(1)求椭圆E的方程;(2)O为坐标原点,⊙![]() 的任意一条切线与椭圆E有两个交点
的任意一条切线与椭圆E有两个交点![]() ,
,![]() 且
且![]() ,求⊙
,求⊙![]() 的半径。
的半径。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年内蒙古呼伦贝尔市高三第三次模拟考试文科数学试卷 题型:解答题
(本小题共12分)如图,已知 ⊥平面
⊥平面 ,
, ∥
∥ ,
, 是正三角形,
是正三角形, ,且
,且 是
是 的中点
的中点

(1)求证: ∥平面
∥平面 ;
;
(2)求证:平面BCE⊥平面 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年内蒙古呼伦贝尔市高三第三次模拟考试文科数学试卷 题型:解答题
(本小题共12分)某中学的高二(1)班男同学有 名,女同学有
名,女同学有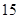 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个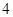 人的课外兴趣小组.
人的课外兴趣小组.
(Ⅰ)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(Ⅱ)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
查看答案和解析>>
科目:高中数学 来源:2010-2011学年甘肃省天水市高三上学期第一阶段性考试理科数学卷 题型:解答题
(本小题共12分)
如图,在正三棱柱ABC—A1B1C1中,点D是棱AB的中点,BC=1,AA1=
(1)求证:BC1//平面A1DC;
(2)求二面角D—A1C—A的大小

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com