Question

已知集合A={x|x²-4mx+2m+6=0}，B={x|x＜0}，若A∩B≠φ，则m的取值范围为________．

Answer 1

m≤-1
分析：由A∩B≠∅，B={x|x＜0}，则方程有负根，我们可根据一元二次方程根的个数的判定方法，我们易得方程有根时m的取值范围，由韦达定理（根与系数的关系），我们先求出方程无负根（即有根，但根均大于等于零）时m的取值范围，进而可求出满足条件的m的取值范围．
解答：∵B={x|x＜0}，且A∩B≠∅，
∴方程x²-4mx+2m+6=0至少存在一个负根
若方程x²-4mx+2m+6=0有实根
则△=（-4m）²-4（2m+6）≥0
即2m²-m-3≥0，解得m≤-1，或m≥
若方程无负根，则

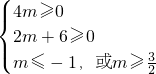
解得m≥
故方程x²-4mx+2m+6=0至少存在一个负根时，m≤-1，
即A∩B≠∅时，则m的取值范围为m≤-1．
故答案为：m≤-1
点评：本题考查的知识点是集合的交集的定义及运算，空集的定义，根的个数及判定，韦达定理，根据B={x|x＜0}，且A∩B≠∅，得到方程x²-4mx+2m+6=0至少存在一个负根，将一个集合问题转化为方程问题，是解答本题的关键．