
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的单调性;
上的单调性;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 上的最小值为3,若存在,求出
上的最小值为3,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)当![]() ,求证:
,求证:![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”,最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?现有这样一个相关的问题:将1到2020这2020个自然数中被5除余3且被7除余2的数按照从小到大的顺序排成一列,构成一个数列,则该数列各项之和为( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() ,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)在平面直角坐标系xOy中,A(﹣2,0),B(0,﹣2),M是曲线C上任意一点,求△ABM面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 与圆
与圆![]() :
: ![]() 相切,且与圆
相切,且与圆![]() :
: ![]() 相内切,记圆心
相内切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .设
.设![]() 为曲线
为曲线![]() 上的一个不在
上的一个不在![]() 轴上的动点,
轴上的动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交曲线
的平行线交曲线![]() 于
于![]() ,
, ![]() 两个不同的点.
两个不同的点.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)试探究![]() 和
和![]() 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
(Ⅲ)记![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明用数列{an}记录某地区2019年12月份31天中每天是否下过雨,方法为:当第k天下过雨时,记ak=1,当第k天没下过雨时,记ak=﹣1(1≤k≤31);他用数列{bn}记录该地区该月每天气象台预报是否有雨,方法为:当预报第k天有雨时,记bk=1,当预报第k天没有雨时,记bk=﹣1(1≤k≤31);记录完毕后,小明计算出a1b1+a2b2+…+a31b31=25,那么该月气象台预报准确的的总天数为_____;若a1b1+a2b2+…+akbk=m,则气象台预报准确的天数为_____(用m,k表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念越来越深入人心,据此,某网站调查了人们对生态文明建设的关注情况,调查数据表明,参与调查的人员中关注生态文明建设的约占80%.现从参与调查的关注生态文明建设的人员中随机选出200人,并将这200人按年龄(单位:岁)分组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65],得到的频率分布直方图如图所示.
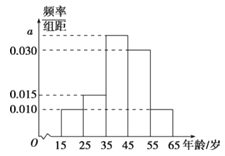
(Ⅰ)求这200人的平均年龄(每一组用该组区间的中点值作为代表)和年龄的中位数(保留一位小数);
(Ⅱ)现在要从年龄在第1,2组的人员中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求抽取的3人中恰有2人的年龄在第2组中的概率;
(Ⅲ)若从所有参与调查的人(人数很多)中任意选出3人,设这3人中关注生态文明建设的人数为X,求随机变量X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() ,
, ![]() ;
;
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且
,且![]() 是单调递增数列,求实数
是单调递增数列,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,
, ![]() ,对于任意给定的正整数
,对于任意给定的正整数![]() ,是否存在正整数
,是否存在正整数![]() 、
、![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 、
、![]() 的值(只要写出一组即可);若不存在,请说明理由;
的值(只要写出一组即可);若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,点
轴非负半轴为极轴建立极坐标系,点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 的延长线上,且满足
的延长线上,且满足![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 面积的最小值。
面积的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com