
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并求出函数![]() 的解析式;
的解析式;
(2)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】某地建一座桥,两端的桥墩已建好,这两墩相距m米,余下工程只需建两端桥墩之间的桥面和桥墩.经测算,一个桥墩的工程费用为256万元;距离为x米的相邻两墩之间的桥面工程费用为(2+![]() )x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.
)x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.
(1)试写出y关于x的函数关系式;
(2)当m=640米时,需新建多少个桥墩才能使y最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 设函数![]()
(1)如果![]() ,那么实数
,那么实数![]() ___;
___;
(2)如果函数![]() 有且仅有两个零点,那么实数
有且仅有两个零点,那么实数![]() 的取值范围是___.
的取值范围是___.
【答案】![]() 或4;
或4;![]()
【解析】
试题分析:由题意![]() ,解得
,解得![]() 或
或![]() ;
;
第二问如图:
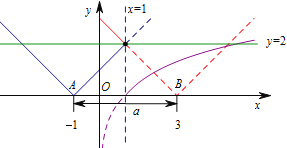
![]() 的图象是由两条以
的图象是由两条以![]() 为顶点的射线组成,当
为顶点的射线组成,当![]() 在A,B 之间(包括
在A,B 之间(包括![]() 不包括
不包括![]() )时,函数
)时,函数![]() 和
和![]() 有两个交点,即
有两个交点,即![]() 有两个零点.所以
有两个零点.所以![]() 的取值范围为
的取值范围为![]() .
.
考点:1.分段函数值;2.函数的零点.
【题型】填空题
【结束】
15
【题目】已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
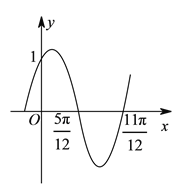
(![]() )求函数
)求函数![]() 的解析式.
的解析式.
(![]() )求函数
)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() ,
,![]() ,
,![]() 为坐标原点,点
为坐标原点,点![]() 满足
满足![]() =
=![]() +
+![]() ,(
,(![]() 为实数);
为实数);
(1)当点![]() 在
在![]() 轴上时,求实数
轴上时,求实数![]() 的值;
的值;
(2)四边形![]() 能否是平行四边形?若是,求实数
能否是平行四边形?若是,求实数![]() 的值;若不是,请说明理由.
的值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数是( )
①如果![]() 、
、![]() 是两条直线,
是两条直线,![]() ,那么
,那么![]() 平行于过
平行于过![]() 的任何一个平面;②如果直线
的任何一个平面;②如果直线![]() 满足
满足![]() ,那么
,那么![]() 与平面
与平面![]() 内的任何一条直线平行;③如果直线
内的任何一条直线平行;③如果直线![]() 、
、![]() 满足
满足![]() ,
,![]() ,则
,则![]() ;④如果直线
;④如果直线![]() 、
、![]() 和平面
和平面![]() 满足
满足![]() ,
,![]() ,
,![]() ,那么
,那么![]() ;⑤如果
;⑤如果![]() 与平面
与平面![]() 内的无数条直线平行,那么直线
内的无数条直线平行,那么直线![]() 必平行于平面
必平行于平面![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的一系列对应值如下表:
的一系列对应值如下表:

(1)根据表格提供的数据求出函数![]() 的一个解析式;
的一个解析式;
(2)根据(1)的结果,若函数![]() 的周期为
的周期为![]() ,当
,当![]() 时,方程
时,方程![]() 恰有两个不同的解,求实数
恰有两个不同的解,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时,某地上班族![]() 中的成员仅以自驾或公交方式通勤,分析显示:当
中的成员仅以自驾或公交方式通勤,分析显示:当![]() 中
中![]() 的成员自驾时,自驾群体的人均通勤时间为
的成员自驾时,自驾群体的人均通勤时间为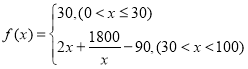 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受![]() 影响,恒为40分钟,试根据上述分析结果回答下列问题:
影响,恒为40分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族![]() 的人均通勤时间
的人均通勤时间![]() 的表达式;并求
的表达式;并求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com