
【题目】如图,圆O为△ABC的外接圆,过点C作圆O的切线交AB的延长线于点D,∠ADC的平分线交AC于点E,∠ACB的平分线交AD于点H. 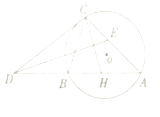
(1)求证:CH⊥DE;
(2)若AE=2CE.证明:DC=2DB.
【答案】
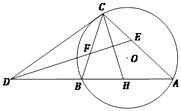
(1)证明:如图,
设DE与BC交于点F,则∠CFE=∠CDF+∠DCF,∠DEC=∠EDA+∠DAE,
因为DC为圆O的切线,
所以∠DCF=∠DAE,
又因DE为∠ADC的平分线,
所以∠CDF=∠EDA,
所以∠DEC=∠CFE
即∠CEF=∠CFE,所以△CFE为等腰三角形,
又因CH为∠ACB的平分线,所以CH⊥EF,
即CH⊥DE
(2)证明:因DC为圆O的切线,
所以DC2=DBDA,
又因DE为∠ADC的平分线,AE=2CE,
所以 ![]() ,所以
,所以 ![]() =2,
=2,
即DC=2DB
【解析】(1)证明∠CEF=∠CFE,所以△CFE为等腰三角形,又因CH为∠ACB的平分线,所以CH⊥EF,即可证明CH⊥DE;(2)证明DC2=DBDA,因DE为∠ADC的平分线,AE=2CE.即可证明:DC=2DB.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】已知四棱柱ABCD﹣A1B1C1D1的底面ABCD为正方形,AA1⊥AC,M、N分别为棱AA1、CC1的中点.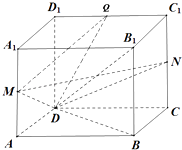
(1)求证:直线MN⊥平面B1BD;
(2)已知AA1=AB,AA1⊥AB,取线段C1D1的中点Q,求二面角Q﹣MD﹣N的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点F1(﹣c,0),F2(c,0)分别是椭圆C: ![]() =1(a>1)的左、右焦点,P为椭圆C上任意一点,且
=1(a>1)的左、右焦点,P为椭圆C上任意一点,且 ![]()
![]() 的最小值为0.
的最小值为0. 
(1)求椭圆C的方程;
(2)如图,动直线l:y=kx+m与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且F1M⊥l,F2N⊥l,求四边形F1MNF2面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率为![]() ,它的一个顶点恰好是抛物线x2=4
,它的一个顶点恰好是抛物线x2=4![]() y的焦点.
y的焦点.
(1)求椭圆C的方程;
(2)直线x=2与椭圆交于P,Q两点,P点位于第一象限,A,B是椭圆上位于直线x=2两侧的动点.
①若直线AB的斜率为![]() ,求四边形APBQ面积的最大值;
,求四边形APBQ面积的最大值;
②当点A,B运动时,满足∠APQ=∠BPQ,问直线AB的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项为﹣6的等差数列{an}的前7项和为0,等比数列{bn}满足b3=a7 , |b3﹣b4|=6.
(1)求数列{bn}的通项公式;
(2)是否存在正整数k,使得数列{ ![]() }的前k项和大于
}的前k项和大于 ![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心在
的圆心在![]() 轴上,并且过
轴上,并且过![]() 两点.
两点.
(1)求圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,那么以
两点,那么以![]() 为直径的圆能否经过原点,若能,请求出直线
为直径的圆能否经过原点,若能,请求出直线![]() 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣
x3﹣ ![]() ax2 , a∈R,
ax2 , a∈R,
(1)当a=2时,求曲线y=f(x)在点(3,f(3))处的切线方程;
(2)设函数g(x)=f(x)+(x﹣a)cosx﹣sinx,讨论g(x)的单调性并判断有无极值,有极值时求出极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(Ⅰ)证明:CE∥平面PAB;
(Ⅱ)求直线CE与平面PBC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com