(1)设C(x,y),由
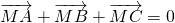
知,
∴M是△ABC的重心,∴
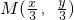
.
∵
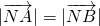
且向量

与

共线,∴N在边AB的中垂线上,
∵
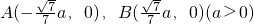
,∴
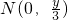
,
又∵
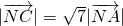
,∴
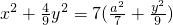
,化简得

,
即所求的轨迹方程是

.
(2)设E(x
1,y
1)、F(x
2,y
2),过点P(0,a)的直线方程为y=kx+a,
代入

得(3-k
2)x
2-2akx-4a
2=0,
∴
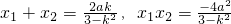
,且△=4a
2k
2+16a
2(3-k
2)>0,解得k
2<4.
∴k
2-3<1,则
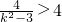
或
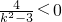
,
∴
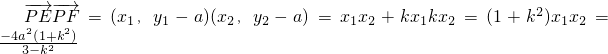
=
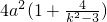
,
则

的取值范围是(-∞,4a
2)∪(20a
2,+∞).
(3)设Q(x
0,y
0)(x
0>0,y
0>0),则
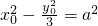
,即y
02=3(x
02-a
02).
当QH⊥x轴时,x
0=2a,y
0=3a,∴∠QGH=

,即∠QHG=2QGH,故猜想λ=2.
当QH不垂直x轴时,tan∠QHG=
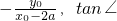
QGH=
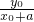
,
∴tan2∠QGH=
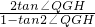
=
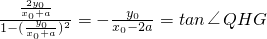
.
又2∠QGH与∠QHG同在
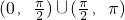
内,
∴2∠QGH=∠QHG.
故存在λ=2,使2∠QGH=∠QHG恒成立.
分析:(1)先设出点C的坐标,根据△ABC的重心的充要条件表示出点M的坐标,再根据点A和B坐标以及距离的关系求出点N的坐标,由两点之间的距离公式代入
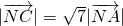
,进行化简求出点C的轨迹方程;
(2)由题意设出点E、F和直线的方程,联立直线方程和轨迹方程,消去y得到关于x的二次方程,根据韦达定理列出两根和以及积的式子,由判别式的符号求出k
2-3的范围,根据向量数量积的坐标运算列出

关于k的式子,根据求出的范围,即求出

的范围;
(3)设出Q的坐标并代入轨迹方程,由特殊情况QH⊥x轴求出λ的值,根据点G和H坐标求出两个角的正切值,由两个角的范围和正切值进行判断是否成立.
点评:本题考查了轨迹方程的求法以及向量数量积的坐标,利用△ABC的重心的充要条件和距离公式求出轨迹方程,主要利用解析法中的设而不求思想,即根据题意列出方程组,根据韦达定理和判别式列出式子,把式子整体代入进行化简,此题综合性强,涉及的知识多,考查了分析问题和解决问题的能力.

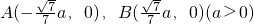 ,两动点M、N满足
,两动点M、N满足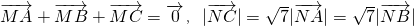 ,向量
,向量 与
与 共线.
共线. 的取值范围.
的取值范围.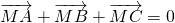 知,
知,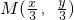 .
.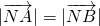 且向量
且向量 与
与 共线,∴N在边AB的中垂线上,
共线,∴N在边AB的中垂线上,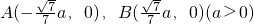 ,∴
,∴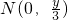 ,
,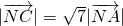 ,∴
,∴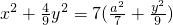 ,化简得
,化简得 ,
, .
. 得(3-k2)x2-2akx-4a2=0,
得(3-k2)x2-2akx-4a2=0,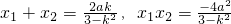 ,且△=4a2k2+16a2(3-k2)>0,解得k2<4.
,且△=4a2k2+16a2(3-k2)>0,解得k2<4.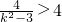 或
或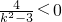 ,
,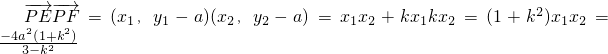
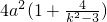 ,
, 的取值范围是(-∞,4a2)∪(20a2,+∞).
的取值范围是(-∞,4a2)∪(20a2,+∞).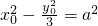 ,即y02=3(x02-a02).
,即y02=3(x02-a02). ,即∠QHG=2QGH,故猜想λ=2.
,即∠QHG=2QGH,故猜想λ=2.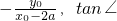 QGH=
QGH=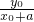 ,
,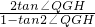 =
=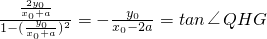 .
.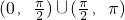 内,
内,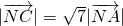 ,进行化简求出点C的轨迹方程;
,进行化简求出点C的轨迹方程; 关于k的式子,根据求出的范围,即求出
关于k的式子,根据求出的范围,即求出 的范围;
的范围;
