
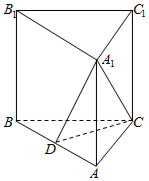
 如图,直三棱柱ABC-A1B1C1中,D是AB的中点,AB=2$\sqrt{2}$,AA1=AC=CB=2.
如图,直三棱柱ABC-A1B1C1中,D是AB的中点,AB=2$\sqrt{2}$,AA1=AC=CB=2.分析 (1)由AA1⊥平面ABC得出AA1⊥CD,由AC=BC得出CD⊥AB,故而CD⊥平面AA1B1B;
(2)由勾股定理的逆定理得出AC⊥BC,计算S△ACD,于是V${\;}_{A-{A}_{1}DC}$=V${\;}_{{A}_{1}-ACD}$=$\frac{1}{3}{S}_{△ACD}•A{A}_{1}$.
解答  证明:(I)∵AA1⊥平面ABC,CD?平面ABC,
证明:(I)∵AA1⊥平面ABC,CD?平面ABC,
∴AA1⊥CD.
∵AC=BC,D为AB的中点,
∴CD⊥AB,
又AB?平面AA1B1B,AA1?平面AA1B1B,AB∩AA1=A,
∴CD⊥平面AA1B1B.
(II)∵AB=2$\sqrt{2}$,AC=CB=2,∴AB2=AC2+BC2,
∴AC⊥BC.
∵D是AB的中点,
∴S△ACD=$\frac{1}{2}{S}_{△ABC}$=$\frac{1}{2}×2×2×\frac{1}{2}$=1.
又AA1⊥平面ABC,
∴V${\;}_{A-{A}_{1}DC}$=V${\;}_{{A}_{1}-ACD}$=$\frac{1}{3}{S}_{△ACD}•A{A}_{1}$=$\frac{1}{3}×1×2$=$\frac{2}{3}$.
点评 本题考查了线面垂直的判定,棱锥的体积计算,属于基础题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:解答题
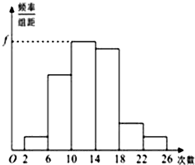 为了解某校学生暑期参加体育锻炼的情况,对某班M名学生暑期参加体育锻炼的次数进行了统计,得到如表的频率分布表与如图直方图:
为了解某校学生暑期参加体育锻炼的情况,对某班M名学生暑期参加体育锻炼的次数进行了统计,得到如表的频率分布表与如图直方图:| 组别 | 锻炼次数 | 频数(人) | 频率 |
| 1 | [2,6) | 2 | 0.04 |
| 2 | [6,10) | 11 | 0.22 |
| 3 | [10,14) | 16 | c |
| 4 | [14,18) | 15 | 0.30 |
| 5 | [18,22) | d | e |
| 6 | [22,26] | 2 | 0.04 |
| 合计 | M | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{10}$) | B. | (1,$\sqrt{3}$) | C. | (1,3) | D. | (1,10) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{12}$+kπ,$\frac{5π}{12}$+kπ](k∈Z) | B. | [-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z) | ||
| C. | [-$\frac{2π}{3}$+4kπ,$\frac{4π}{3}$+4kπ](k∈Z) | D. | [-$\frac{5π}{6}$+4kπ,$\frac{7π}{6}$+4kπ](k∈Z) |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:填空题
设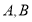 为抛物线
为抛物线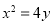 上的两动点,且线段
上的两动点,且线段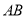 的长为6,
的长为6,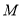 为线段
为线段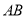 的中点,则点
的中点,则点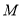 到
到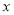 轴的最短距离为 .
轴的最短距离为 .
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:填空题
若集合 满足
满足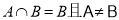 ,则命题“
,则命题“ ”是命题“
”是命题“ ”的 条件.(填“充分不必要”,“必要不充分”,“充要”)
”的 条件.(填“充分不必要”,“必要不充分”,“充要”)
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,$\frac{3}{2}$) | C. | ($\frac{1}{2}$,$\frac{5}{2}$) | D. | ($\frac{3}{2}$,$\frac{5}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com