
在 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为
(Ⅰ)叙述并证明正弦定理;
(Ⅱ)设 ,
, ,求
,求 的值.
的值.
(Ⅰ)证明见解析;(Ⅱ) 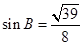 .
.
解析试题分析:(Ⅰ)正弦定理: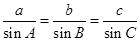 ,利用三角形的外接圆证明正弦定理. 设
,利用三角形的外接圆证明正弦定理. 设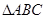 的外接圆的半径为
的外接圆的半径为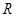 ,连接
,连接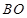 并延长交圆
并延长交圆 于点
于点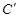 ,则
,则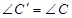 ,直径所对的圆周角
,直径所对的圆周角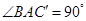 ,在直角三角形
,在直角三角形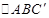 中,
中,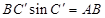 ,从而得到
,从而得到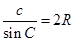 ,同理可证
,同理可证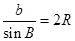 ,
,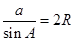 ,则正弦定理得证;(Ⅱ)先由正弦定理将
,则正弦定理得证;(Ⅱ)先由正弦定理将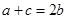 化为
化为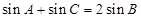 ①,再依据和差化积公式,同角三角函数间的关系,特殊角的三角函数值将①式化简,得到
①,再依据和差化积公式,同角三角函数间的关系,特殊角的三角函数值将①式化简,得到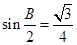 ,则
,则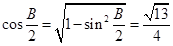 ,再由二倍角公式
,再由二倍角公式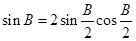 求解.
求解.
试题解析:(Ⅰ) 正弦定理: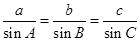 .
.
证明:设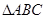 的外接圆的半径为
的外接圆的半径为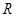 ,连接
,连接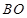 并延长交圆
并延长交圆 于点
于点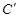 ,如图所示:
,如图所示: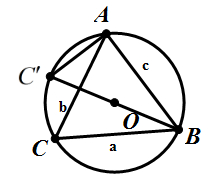
则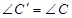 ,
,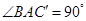 ,在
,在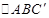 中,
中,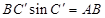 ,即
,即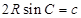 ,则有
,则有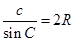 ,同理可得
,同理可得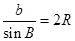 ,
,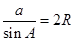 ,所以
,所以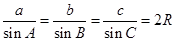 .
.
(Ⅱ)∵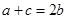 ,由正弦定理得,
,由正弦定理得,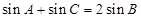 ,
, ,
,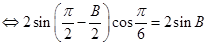 ,
,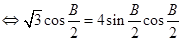 ,
,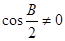 ,
,
解得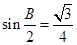 ,
,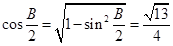 ,
,
∴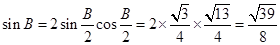 .
.
考点:1.正弦定理;2.解三角形;3.同角三角函数间的关系;4.和差化积公式;5.二倍角公式


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com