练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    判断下列函数是否存在反函数:

    (1)y=(x∈R且x≠-2)；

    (2)y=x2-2x(x∈R)；

    (3)y=x2-2x(x≤1).

    思路解析:反函数也是函数.根据函数的定义,判断函数是否具有反函数,关键在于该函数在所给的定义域内是否满足“x与y是一一对应”,即对于值域中任意一个y值,是否都存在唯一的x值和它对应.判断时,可以借助于函数的图象,也可以借助于函数的性质.

    解:(1)有反函数.

    (2)无反函数.

    (3)有反函数.

    误区警示

    并不是所有函数都具有反函数,设函数y=f(x)是定义在A上的函数,若对任意x1,x2∈A,当x1≠x2时,都有f(x1)≠f(x2),即不同的自变量x对应不同的函数值y,而不同的y值也对应不同的x的值时,此函数才具有反函数,比如:

    函数y=x2在区间［-1,2］上不存在反函数,是由于x∈［-1,2］时,存在互为相反的两个x,都能得到相同的y=x2值,故不存在逆映射,也就不存在反函数了；

    函数y=x2在区间［0,2］上,根据图象可知,任意不同的自变量x的值,都存在不同的y值和它对应,故存在反函数y=(0≤x≤4).

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    判断下列函数是否存在零点，如果存在，请求出．
    （1）f（x）=-8x2+7x+1；
    （2）f（x）=x2+x+2；
    （3）f（x）=
    x2+4x-12x-2
    ；
    （4）f（9x）=3x+1-7；
    （5）f（x）=log5（2x-3）．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    判断下列函数是否存在零点，如果存在，请求出．
    （1）f（x）=-8x2+7x+1；
    （2）f（x）=x2+x+2；
    （3）f（x）=
    x2+4x-12
    x-2
    ；
    （4）f（9x）=3x+1-7；
    （5）f（x）=log5（2x-3）．

    查看答案和解析>>

    科目：高中数学 来源：同步题 题型：解答题

    判断下列函数是否存在零点，如果存在，请求出．
    (1)f(x)=-8x2+7x+1；
    (2)f(x)=x2+x+2；
    (3)f(x)=x3+1。

    查看答案和解析>>

    科目：高中数学 来源：同步题 题型：解答题

    判断下列函数是否存在零点，如果存在，请求出．
    (1)f(x)=-8x2+7x+1；
    (2)f(x)=x2+x+2；
    (3)f(x)=x3+1；
    (4)。

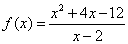    查看答案和解析>>

    同步练习册答案