Question

【题目】已知函数 ，g（x）=b（x+1），其中a≠0，b≠0
（1）若a=b，讨论F（x）=f（x）﹣g（x）的单调区间；
（2）已知函数f（x）的曲线与函数g（x）的曲线有两个交点，设两个交点的横坐标分别为x1 ， x2 ， 证明： ．

Answer 1

【答案】
（1）解：由已知得 ，

∴ ，

当0＜x＜1时，∵1﹣x2＞0，﹣lnx＞0，∴1﹣x2﹣lnx＞0，；

当x＞1时，∵1﹣x2＜0，﹣lnx＜0，∴1﹣x2﹣lnx＜0．

故若a＞0，F（x）在（0，1）上单调递增，在（1，+∞）上单调递减；

故若a＜0，F（x）在（0，1）上单调递减，在（1，+∞）上单调递增

（2）解：不妨设x1＞x2，依题意 ，

∴ ，同理得

由①﹣②得，∴ ，

∴ ，

∴ ，

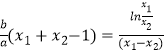故只需证 ，

取∴ ，即只需证明 成立，

即只需证 成立，

∵ ，

∴p（t）在区间[1，+∞）上单调递增，

∴p（t）＞p（1）=0，t＞1成立，

故原命题得证

【解析】（1）求出函数的导数，解关于导函数的不等式，求出函数的单调区间即可（2）问题转化为证 ， ，只需证明 成立，根据函数的单调性证明即可．
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减才能正确解答此题．