
分析 原方程等价于x3+a=$\frac{4}{x}$,原方程的实根是曲线y=x3+a与曲线y=$\frac{4}{x}$ 的交点的横坐标,分别作出左右两边函数的图象:分a>0与a<0讨论,可得答案.
解答 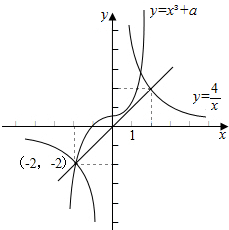 解:方程的根显然x≠0,原方程等价于x3+a=$\frac{4}{x}$,
解:方程的根显然x≠0,原方程等价于x3+a=$\frac{4}{x}$,
原方程的实根是曲线y=x3+a与曲线y=$\frac{4}{x}$ 的交点的横坐标,
而曲线y=x3+a是由曲线y=x3向上或向下平移|a|个单位而得到的,
若交点$({x}_{i},\frac{4}{{x}_{i}})$(i=1,2,…,k)均在直线y=x的同侧,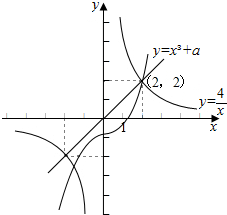 因直线y=x与y=$\frac{4}{x}$交点为:(-2,-2),(2,2);
因直线y=x与y=$\frac{4}{x}$交点为:(-2,-2),(2,2);
所以结合图象可得$\left\{\begin{array}{l}{a>0}\\{{(-2)}^{3}+a>-2}\\{x<-2}\end{array}\right.$或$\left\{\begin{array}{l}{a<0}\\{{2}^{3}+a<2}\\{x>2}\end{array}\right.$,
解得a>6或a<-6.
故答案为:a>6或a<-6.
点评 本题综合考查函数与方程的应用,数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质.考查学生的转化二行推理能力.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:解答题
| x | $\frac{π}{2}$ | 2π | $\frac{7π}{2}$ | 5π | $\frac{13π}{2}$ |
| y | 0 | 2 | 0 | -2 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
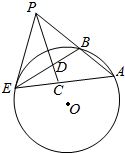 如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D.
如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | -4$\sqrt{3}$ | C. | ±4$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | 0 | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)有最小值2 | B. | 函数f(x)有最大值2 | C. | 函数f(x)有最小值3 | D. | 函数f(x)有最大值3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com