
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,求证:过点
时,求证:过点![]() 有三条直线与曲线
有三条直线与曲线![]() 相切;
相切;
(Ⅱ)当![]() 时,
时, ![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(I)详见解析;(II)![]() .
.
【解析】试题分析:
(1)首先对函数求导,写出切线方程,讨论方程根的分布可得过点![]() 有三条直线与曲线
有三条直线与曲线![]() 相切;
相切;
(2)利用题意构造函数![]() ,由新函数的性质可得实数
,由新函数的性质可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:解法一:(Ⅰ)当![]() 时,
时, ![]() ,
,
![]()
![]()
设直线与曲线![]() 相切,其切点为
相切,其切点为![]() ,
,
则曲线![]() 在点
在点![]() 处的切线方程为:
处的切线方程为: ![]() ,
,
因为切线过点![]() ,所以
,所以![]() ,
,
即![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,
,
设![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
, ![]()
∴![]() 在三个区间
在三个区间![]() 上至少各有一个根
上至少各有一个根
又因为一元三次方程至多有三个根,所以方程![]() 恰有三个根,
恰有三个根,
故过点![]() 有三条直线与曲线
有三条直线与曲线![]() 相切.
相切.
(Ⅱ)∵当![]() 时,
时, ![]() ,即当
,即当![]() 时,
时, ![]()
∴当![]() 时,
时, ![]() ,
,
设![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() .
.
(1)当![]() 时,∵
时,∵![]() ,∴
,∴![]() ,从而
,从而![]() (当且仅当
(当且仅当![]() 时,等号成立)
时,等号成立)
∴![]() 在
在![]() 上单调递增,
上单调递增,
又∵![]() ,∴当
,∴当![]() 时,
时, ![]() ,从而当
,从而当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上单调递减,又∵
上单调递减,又∵![]() ,
,
从而当![]() 时,
时, ![]() ,即
,即![]()
于是当![]() 时,
时, ![]() .
.
(2)当![]() 时,令
时,令![]() ,得
,得![]() ,∴
,∴![]() ,
,
故当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减,
又∵![]() ,∴当
,∴当![]() 时,
时, ![]() ,
,
从而当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上单调递增,又∵
上单调递增,又∵![]() ,
,
从而当![]() 时,
时, ![]() ,即
,即![]()
于是当![]() 时,
时, ![]() ,
,
综合得![]() 的取值范围为
的取值范围为![]() .
.
解法二:(Ⅰ)当![]() 时,
时, ![]() ,
,
![]()
![]() ,
,
设直线与曲线![]() 相切,其切点为
相切,其切点为![]() ,
,
则曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
因为切线过点![]() ,所以
,所以![]() ,
,
即![]()
![]() ,
,
∵![]() ,∴
,∴![]()
设![]() ,则
,则![]() ,令
,令![]() 得
得![]()
当![]() 变化时,
变化时, ![]() ,
, ![]() 变化情况如下表:
变化情况如下表:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| ↗ | 极大值
| ↘ | 极小值 | ↗ |
∴![]() 恰有三个根,
恰有三个根,
故过点![]() 有三条直线与曲线
有三条直线与曲线![]() 相切.
相切.
(Ⅱ)同解法一.


科目:高中数学 来源: 题型:
【题目】
如图,⊙O内切于△ABC的边于D,E,F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G.
(Ⅰ)求证:圆心O在直线AD上;
(Ⅱ)求证:点C是线段GD的中点.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为落实《课标》所倡导的课程理念,切实提高学生的综合素质,某校高二年级开设“趣味数学”、“趣味物理”、“趣味化学”3门任意选修课程,供年级300位文科生自由选择2门(不可多选或少选),选课情况如下表:

(Ⅰ)为了解学生选课情况,现采用分层抽样方法抽取了三科作业共50本,统计发现“趣味物理”有18本,试根据这一数据估计![]() ,
, ![]() 的值;
的值;
(Ⅱ)为方便开课,学校要求![]() ,
, ![]() ,计算
,计算![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点. 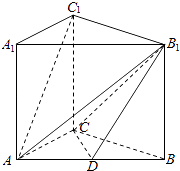
(1)求证:AC1∥平面CDB1
(2)求证:AC⊥BC1
(3)求直线AB1与平面BB1C1C所成的角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,函数
,函数![]() ,且
,且![]() 图象上一个最高点为
图象上一个最高点为![]() 与
与![]() 最近的一个最低点的坐标为
最近的一个最低点的坐标为![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)设![]() 为常数,判断方程
为常数,判断方程![]() 在区间
在区间![]() 上的解的个数;
上的解的个数;
(Ⅲ)在锐角![]() 中,若
中,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x|,g(x)=lg(ax2﹣4x+1),若对任意x1∈R,都存在在x2∈R,使f(x1)=g(x2),则实数a的取值范围是( )
A.(﹣∞,4]
B.(0,4]
C.(﹣4,0]
D.[0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,集合M={x|f(x)=0}={x1 , x2 , x3 , x4 , x5}N* , 设c1≥c2≥c3 , 则c1﹣c3=( )
,集合M={x|f(x)=0}={x1 , x2 , x3 , x4 , x5}N* , 设c1≥c2≥c3 , 则c1﹣c3=( )
A.6
B.8
C.2
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017衡阳第二次联考】已知四棱锥![]() 中,底面为矩形,
中,底面为矩形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 上一点,
上一点, ![]() 为
为![]() 的中点.
的中点.
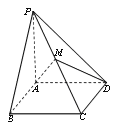
(1)在图中作出平面![]() 与
与![]() 的交点
的交点![]() ,并指出点
,并指出点![]() 所在位置(不要求给出理由);
所在位置(不要求给出理由);
(2)求平面![]() 将四棱锥
将四棱锥![]() 分成上下两部分的体积比.
分成上下两部分的体积比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com